题目内容
16.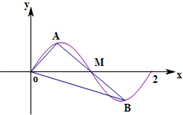 如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )
如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用三角函数的图象的性质设出A(x1,sinπx1),B(2-x1,-sinπx1),
$\overrightarrow{OA}$=(x1,sinπx1),$\overrightarrow{OB}$=(2-x1,-sinπx1),根据M(1,0)是AB的中点,得出$\overrightarrow{OM}$=$\frac{1}{2}$($\overrightarrow{OA}$$+\overrightarrow{OB}$),
利用向量的数量积求解即可.
解答 解:∵ 过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点
过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点
∴根据三角函数的对称性得出;A(x1,sinπx1),B(2-x1,-sinπx1)
∴$\overrightarrow{OA}$=(x1,sinπx1),$\overrightarrow{OB}$=(2-x1,-sinπx1)
$\overrightarrow{OA}$$+\overrightarrow{OB}$=(2,0)
∵M(1,0)是AB的中点,
∴$\overrightarrow{OM}$=$\frac{1}{2}$($\overrightarrow{OA}$$+\overrightarrow{OB}$),
∴$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)=$\frac{(\overrightarrow{OA}+\overrightarrow{OB})^{2}}{2}$=$\frac{4}{2}$=2,
故选:B.
点评 本题考察了三角函数图象的性质,平面向量的运用,考察了学生对于数形结合的思想的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.在平面直角坐标系xoy中,A、B、C是圆x2+y2=1上相异三点,若存在正实数λ,μ,使得$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,则λ2+(μ-3)2的取值范围是( )
| A. | [0,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (8,+∞) |
4.极坐标方程ρ=2$\sqrt{2}$cos($\frac{π}{4}$-θ)表示图形的面积是( )
| A. | 2 | B. | 2π | C. | 4 | D. | 4π |
1.已知集合A={x|$\frac{x-1}{x+2}$≥0},B={x|x≤a},若A∩B=B,则a的取值范围是( )
| A. | a≥1 | B. | a≥2 | C. | a≤-2 | D. | a<-2 |
8.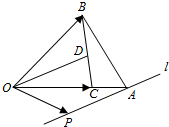 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
6.已知集合A={x|1≤x≤3},B={-1,1,2,3},则A∩B等于( )
| A. | {1,2} | B. | {2,3} | C. | {1,2,3} | D. | {-1,1,2,3} |