题目内容
19.已知函数y=f(x-1)定义域是[-1,3],则y=f(2x+1)的定义域是[-$\frac{3}{2}$,$\frac{1}{2}$].分析 根据复合函数定义域之间的关系进行求解即可.
解答 解:∵函数y=f(x-1)定义域是[-1,3],
∴-1≤x≤3,则-2≤x-1≤2,
即函数f(x)的定义域为[-2,2],
由-2≤2x+1≤2,
得-$\frac{3}{2}$≤x≤$\frac{1}{2}$,
即函数的定义域为[-$\frac{3}{2}$,$\frac{1}{2}$],
故答案为:[-$\frac{3}{2}$,$\frac{1}{2}$].
点评 本题主要考查函数的定义域的求解,要求熟练掌握复合函数定义域之间的关系.

练习册系列答案
相关题目
9.若过A(-2,m)和B(m,4)的直线与斜率为-2的直线平行,则m的值为( )
| A. | -8 | B. | 0 | C. | 2 | D. | 10 |
7.在平面直角坐标系xoy中,A、B、C是圆x2+y2=1上相异三点,若存在正实数λ,μ,使得$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,则λ2+(μ-3)2的取值范围是( )
| A. | [0,+∞) | B. | (2,+∞) | C. | [2,+∞) | D. | (8,+∞) |
4.极坐标方程ρ=2$\sqrt{2}$cos($\frac{π}{4}$-θ)表示图形的面积是( )
| A. | 2 | B. | 2π | C. | 4 | D. | 4π |
8.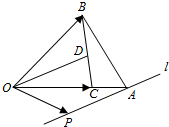 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |