题目内容
18.规定$A_x^m=x(x-1)…(x-m+1)$,其中x∈R,m为正整数,且$A_x^0$=1,这是排列数A${\;}_{n}^{m}$(n,m是正整数,n≤m)的一种推广.(Ⅰ) 求A${\;}_{-9}^{3}$的值;
(Ⅱ)排列数的性质:A${\;}_{n}^{m}$+mA${\;}_{n}^{m-1}$=A${\;}_{n+1}^{m}$(其中m,n是正整数).是否都能推广到A${\;}_{x}^{m}$(x∈R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(Ⅲ)已知函数f(x)=A${\;}_{x}^{3}$-4lnx-m,试讨论函数f(x)的零点个数.
分析 (Ⅰ)根据题目中的公式,计算A${\;}_{-9}^{3}$的值即可;
(Ⅱ)性质可推广,写出推广的形式是$A_x^m$$+mA_x^{m-1}$=$A_{x+1}^m$(x∈R,m∈N*),再证明即可:
(Ⅲ)化简f(x),构造函数g(x),由f(x)零点的个数转化为求g(x)与y=m交点的个数即可.
解答 解:(Ⅰ)根据题意,得;
$A_{-9}^3=-9×(-10)×(-11)=-990$;…(2分)
(Ⅱ)性质可推广,推广的形式是$A_x^m$$+mA_x^{m-1}$=$A_{x+1}^m$(x∈R,m∈N*); …(4分)
证明:当m=1时,左边=$A_x^1+A_x^0=x+1=A_{x+1}^1$=右边,等式成立;
当m≥2时,左边=x(x-1)…(x-m+1)+mx(x-1)…(x-m+2)
=x(x-1)…(x-m+2)(x-m+1+m)
=(x+1)x(x-1)…(x-m+2)
=(x+1)x(x-1)…[(x+1)-m+1)]
=$A_{x+1}^m$=右边;
因此,$A_x^m$$+mA_x^{m-1}$=$A_{x+1}^m$(x∈R,m∈N*)成立;…(7分)
(Ⅲ)$f(x)=A_x^3-4lnx-m=x(x-1)(x-2)-4lnx-m={x^3}-3{x^2}+2x-4lnx-m$
设函数g(x)=x3-3x2+2x-4lnx,g(x)的定义域为(0,+∞),…(8分)
则函数f(x)零点的个数等价于函数g(x)与y=m公共点的个数;${g^'}(x)=3{x^2}-6x+2-\frac{4}{x}=\frac{{3{x^3}-6{x^2}+2x-4}}{x}=\frac{{3{x^2}(x-2)+2(x-2)}}{x}=\frac{{(x-2)(3{x^2}+2)}}{x}$,
令g′(x)=0,得x=2,所以g(x)在(0,2)上单减,在(2,+∞)上单增;
故g(x)的最小值为g(2)=-4ln2;…(10分)
∴当m<-4ln2时,函数g(x)与y=m没有公共点,即函数f(x)不存在零点,
当m=-4ln2时,函数g(x)与y=m有一个公共点,即函数f(x)有且只有一个零点,
当m>-4ln2时,函数g(x)与y=m有两个公共点,即函数f(x)有且只有两个零点.
…(12分)
点评 本题考查了新定义的应用问题,也考查了函数的性质与应用问题,考查了导数的综合应用问题,考查了排列数的应用问题,是综合性问题.

| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |
| B. | “若θ=$\frac{π}{3}$,则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$,则cosθ≠$\frac{1}{2}$” | |
| C. | 已知向量$\overrightarrow{a}$、$\overrightarrow{b}$为非零向量,则“$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$$•\overrightarrow{b}$<0” | |
| D. | 若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1>0 |
| A. | y=±2x | B. | y=±x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
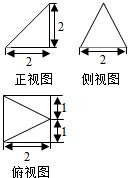 已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.
已知某几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体得体积是( )cm2.| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 2 | D. | 4 |
| A. | -1 | B. | 1 | C. | 3 | D. | 0或3 |
| A. | $\frac{f(m)}{m}<\frac{f(n)}{n}$ | B. | $\frac{f(m)}{m}>\frac{f(n)}{n}$ | C. | $\frac{f(m)}{n}>\frac{3f(n)}{m}$ | D. | $\frac{f(m)}{n}<\frac{f(n)}{m}$ |