题目内容
13．证明和差化积公式：sinx+siny=2sin$\frac{x+y}{2}$cos$\frac{x-y}{2}$．分析 灵活应用三角函数和差公式，即可证明．
解答 证明：sin（α+β）=sinαcosβ+cosαsinβ，
sin（α-β）=sinαcosβ-cosαsinβ，
两式相加得：sin（α+β）+sin（α-β）=2sinαcosβ，
令α+β=x，a-β=y，
则a=$\frac{x+y}{2}$，β=$\frac{x-y}{2}$，
∴sinx+siny=2sin$\frac{x+y}{2}$cos$\frac{x-y}{2}$．
点评 本题考查了三角函数的和差化积公式的证明，属于基础题．
练习册系列答案
相关题目
1．
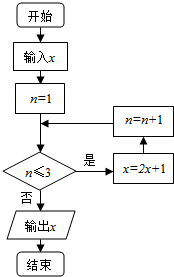已知实数x∈[1，9]，执行如图所示的程序框图，则输出的x不小于55的概率为（ ）
已知实数x∈[1，9]，执行如图所示的程序框图，则输出的x不小于55的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{8}$ | D． | $\frac{5}{8}$ |
1．
将非零自然数列按一定的规则排成如图所示的三角形数列表（每一行比上一行多一个数），设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，如a42=8，若aij=2014则i，j的值分别为（ ）
将非零自然数列按一定的规则排成如图所示的三角形数列表（每一行比上一行多一个数），设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，如a42=8，若aij=2014则i，j的值分别为（ ）| A． | i=62，j=15 | B． | i=62，j=14 | C． | i=64，j=14 | D． | i=64，j=15 |