题目内容
若椭圆 =1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
=1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
 =1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
=1的焦距为2,求椭圆上的一点到两个焦点的距离之和.2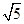 或4
或4
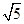 或4
或4学生错解:解:∵2c=2,即c=1,∴m-4=1,∴a=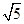 ,则椭圆上的一点到两个焦点的距离之和为2
,则椭圆上的一点到两个焦点的距离之和为2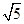 .
.
审题引导:(1)椭圆的定义;(2)椭圆中参数a,b,c满足a2-b2=c2;
(3)焦点在x轴与焦点在y轴上的椭圆的标准方程的区别.
规范解答:解:∵2c=2,即c=1,(4分)
∴当焦点在x轴上时,m-4=1,∴a=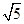 ,(6分)
,(6分)
则椭圆上的一点到两个焦点的距离之和为2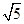 ;(8分)
;(8分)
同理,当焦点在y轴上时,4-m=1,∴b=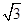 ,a=2,(10分)
,a=2,(10分)
则椭圆上的一点到两个焦点的距离之和为4,(12分)
∴椭圆上的一点到两个焦点的距离之和为2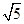 或4.(14分)
或4.(14分)
错因分析:本题考查了椭圆的定义及标准方程,易错原因是忽略椭圆焦点位置对参数的影响.当椭圆焦点位置不确定时,一般要分类讨论.
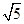 ,则椭圆上的一点到两个焦点的距离之和为2
,则椭圆上的一点到两个焦点的距离之和为2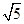 .
.审题引导:(1)椭圆的定义;(2)椭圆中参数a,b,c满足a2-b2=c2;
(3)焦点在x轴与焦点在y轴上的椭圆的标准方程的区别.
规范解答:解:∵2c=2,即c=1,(4分)
∴当焦点在x轴上时,m-4=1,∴a=
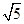 ,(6分)
,(6分)则椭圆上的一点到两个焦点的距离之和为2
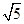 ;(8分)
;(8分)同理,当焦点在y轴上时,4-m=1,∴b=
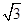 ,a=2,(10分)
,a=2,(10分)则椭圆上的一点到两个焦点的距离之和为4,(12分)
∴椭圆上的一点到两个焦点的距离之和为2
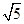 或4.(14分)
或4.(14分)错因分析:本题考查了椭圆的定义及标准方程,易错原因是忽略椭圆焦点位置对参数的影响.当椭圆焦点位置不确定时,一般要分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的焦点在
的焦点在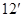 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
. 的方程;
的方程; 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 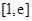 为原点,在
为原点,在 、
、 点的点
点的点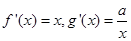 、
、 ,使得
,使得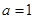 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围. 的左、右焦点分别为
的左、右焦点分别为 、
、 , 焦距为2,过
, 焦距为2,过 为3
为3  交椭圆于A、B两点,判断是否存在直线
交椭圆于A、B两点,判断是否存在直线 为钝角,若存在,求出直线
为钝角,若存在,求出直线 的取值范围
的取值范围 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
,以原点为圆心,椭圆C的短半轴长为半径的圆与直线x-y+2=0相切.
 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E. 的取值范围.
的取值范围. +y2=1的左右焦点,点P在椭圆上运动.则
+y2=1的左右焦点,点P在椭圆上运动.则 的最大值是________.
的最大值是________. ,焦距为2
,焦距为2 ;
;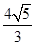 和
和 ,过P点作长轴的垂线恰好过椭圆的一个焦点.
,过P点作长轴的垂线恰好过椭圆的一个焦点.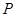 是椭圆
是椭圆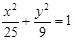 上的点,
上的点, 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若 ,则
,则 的面积为( )
的面积为( )


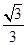
 +
+ =1(a>b>0)的左焦点为F,离心率为
=1(a>b>0)的左焦点为F,离心率为 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为 .
. ·
· +
+ ·
· =8,求k的值.
=8,求k的值.