题目内容
函数f(x)＝3x2＋ln x－2x的极值点的个数是( )
| A．0 | B．1 |
| C．2 | D．无数个 |
A
函数定义域为(0，＋∞)，
且f′(x)＝6x＋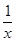
－2＝
.
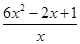由于x>0，g(x)＝6x2－2x＋1中Δ＝－20<0，
所以g(x)>0恒成立，故f′(x)>0恒成立．
即f(x)在定义域上单调递增，无极值点．
且f′(x)＝6x＋
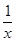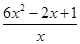－2＝.由于x>0，g(x)＝6x2－2x＋1中Δ＝－20<0，
所以g(x)>0恒成立，故f′(x)>0恒成立．
即f(x)在定义域上单调递增，无极值点．
练习册系列答案
相关题目
x2－(a＋1)x(a>0，a为常数)．
x2－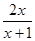
－
.
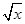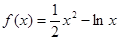的单调递减区间为（ ）
1,1）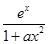
，其中a为正实数．
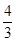时，求f(x)的极值点；②若f(x)为R上的单调函数，求a的取值范围．
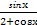的单调递增区间是 .
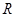上的函数
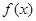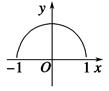
，其导函数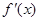
的图像如图所示，则下列叙述正确的是（ ）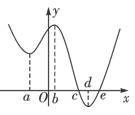
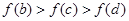
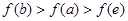
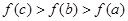
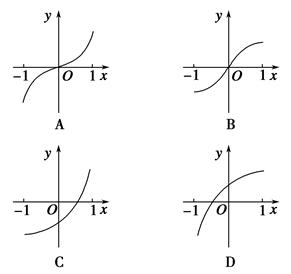
x2－ln x的单调递减区间为 ( )． 
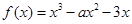在区间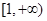
上是增函数，则实数
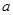的取值范围是 ．