题目内容
5.数列{an}的前几项和为Sn,满足(2t+3)(Sn+1-1)=(3t+4)Sn,a1=1,其中t>0(1)若t为常数,证明:数列{an}为等比数列;
(2)若t为变量,记数列{an}的公比为f(t),数列{bn}满足b1=2,bn+1=f(bn),求b2,b3,试判定bn与$\sqrt{2}$的大小,并加以证明.
分析 (1)利用等比数列的定义,证明$\frac{{{a_{n+1}}}}{a_n}=\frac{3t+4}{2t+3}$,即可证明数列{an}为等比数列;
(2)猜想:bn>$\sqrt{2}$,用数学归纳法证明即可.
解答 解:(1)当n=1时,${a_2}=\frac{3t+4}{2t+3}$
当n≥2时,(2t+3)(sn-1)=(3t+4)sn-1①(2t+3)(sn+1-1)=(3t+4)sn②
②-①得:(2t+3)an+1=(3t+4)an
∴$\frac{{{a_{n+1}}}}{a_n}=\frac{3t+4}{2t+3}$(n≥2)---------4分
又 $\frac{a_2}{a_1}=\frac{3t+4}{2t+3}$
故{an}是等比数列---------------6分
(2)${b_{n+1}}=\frac{{3{b_n}+4}}{{2{b_n}+3}}$${b_2}=\frac{10}{7},{b_3}=\frac{58}{41}$
猜想:bn>$\sqrt{2}$------------8分
下面用数学归纳法证明:
①当n=1,b1=2,则b1>$\sqrt{2}$成立
②假设当n=k时,bk>$\sqrt{2}$
当n=k+1时,${b_{k+1}}=\frac{{3{b_k}+4}}{{2{b_k}+3}}$${b_{k+1}}-\sqrt{2}=\frac{{3{b_k}+4}}{{2{b_k}+3}}-\sqrt{2}$=$\frac{{({3-2\sqrt{2}}){b_k}+({4-3\sqrt{2}})}}{{2{b_k}+3}}$=$\frac{{({3-2\sqrt{2}})({{b_k}-\sqrt{2}})}}{{2{b_k}+3}}$>0${b_{k+1}}≥\sqrt{2}$,即 n=k+1,结论也成立
由①②知:bn>$\sqrt{2}$----------12分.
点评 本题考查等比数列的证明,考查数学归纳法,考查学生分析解决问题的能力,属于中档题.

| A. | 5 | B. | -5 | C. | 0 | D. | 1 |
| A. | 3 | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | $\sqrt{5}$ |
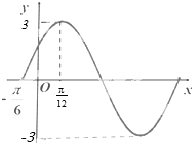 已知函数f(x)=Asin(ωx+φ)的图象如图所示.
已知函数f(x)=Asin(ωx+φ)的图象如图所示.