题目内容
13.若曲线y=x2在点P处的切线斜率为1,则点P的坐标为($\frac{1}{2}$,$\frac{1}{4}$).分析 设切点的坐标为(a,a2),根据函数在某一点的导数的几何意义,可得2a=1,求得a的值,可得点P的坐标.
解答 解:设切点的坐标为(a,a2),则根据曲线y=x2在点P处的切线斜率为1,可得2a=1,求得a=$\frac{1}{2}$,
故切点的坐标为($\frac{1}{2}$,$\frac{1}{4}$),
故答案为:($\frac{1}{2}$,$\frac{1}{4}$).
点评 本题主要考查函数在某一点的导数的几何意义,属于基础题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
3.已知全集U={1,2,3,4,5,6,7,8},集合A={1,4,7},集合B={1,3,4,6,8},则(∁UA)∩B=( )
| A. | {1,4} | B. | {3,6,8} | C. | {1,2,4,5,7} | D. | {2,3,5,6,7,8} |
1.函数$y=sin(2x+\frac{5π}{2})$的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
18.已知三棱锥P-ABC的底面△ABC是正三角形,且PA=PB=PC,E、F是棱PA、BC的中点,记EF与平面PAB所成的角为α,EF与平面ABC所成的角为β,则α+β( )
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | ||
| C. | 大于$\frac{π}{2}$ | D. | 与$\frac{π}{2}$的大小关系不能确定 |
2.一个用流程图表示的算法如图所示,则其运行后输出的结果为( )
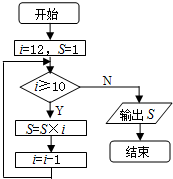

| A. | 1320 | B. | 11880 | C. | 132 | D. | 以上都不对 |
3.已知直线l,平面α、β、γ,则下列能推出α∥β的条件是( )
| A. | l⊥α,l∥β | B. | α∥γ,β∥γ | C. | α⊥γ,β⊥γ | D. | l∥α,l∥β |