题目内容
10.有下列说法:①已知α为第二象限角,则$\frac{α}{2}$为第一或第三象限角;
②已知λ为实数,$\overrightarrow a$为平面内任一向量,则$λ\overrightarrow a$的模为$λ|{\overrightarrow a}|$;
③△ABC中,若tanA•tanC>1,则△ABC为锐角三角形;
④已知O为△ABC所在平面内一点,且$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}=\overrightarrow{OC}•\overrightarrow{OA}$,则点O是△ABC的重心.则正确的序号是①③.
分析 对四个选项分别进行判断,即可得出结论.
解答 解:①∵角α的终边在第二象限,∴2kπ+$\frac{π}{2}$<α<2kπ+π,k∈Z,∴kπ+$\frac{π}{4}$<$\frac{α}{2}$<kπ+$\frac{π}{2}$,
当k为偶数时,2nπ+$\frac{π}{4}$<$\frac{α}{2}$<2nπ+$\frac{π}{2}$,n∈Z,得$\frac{α}{2}$是第一象限角;当k为奇数时,(2n+1)π+$\frac{π}{4}$<$\frac{α}{2}$<(2n+1)π+$\frac{π}{2}$,n∈Z,得$\frac{α}{2}$是第三象限角,故正确;
②已知λ为实数,$\overrightarrow a$为平面内任一向量,则$λ\overrightarrow a$的模为|$λ|{\overrightarrow a}|$|,故不正确;
③△ABC中,若tanA•tanC>1,则cos(A+C)<0,∴B为锐角,tanA•tanC>1,∴A,C为锐角,∴△ABC为锐角三角形,故正确;
④已知O为△ABC所在平面内一点,且$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}=\overrightarrow{OC}•\overrightarrow{OA}$,则点O是△ABC的垂心,故不正确.
故答案为:①③.
点评 本题考查命题的真假判断,考查学生分析解决问题的能力,知识综合性强.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
1.函数$y=sin(2x+\frac{5π}{2})$的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
18.已知三棱锥P-ABC的底面△ABC是正三角形,且PA=PB=PC,E、F是棱PA、BC的中点,记EF与平面PAB所成的角为α,EF与平面ABC所成的角为β,则α+β( )
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | ||
| C. | 大于$\frac{π}{2}$ | D. | 与$\frac{π}{2}$的大小关系不能确定 |
2.一个用流程图表示的算法如图所示,则其运行后输出的结果为( )


| A. | 1320 | B. | 11880 | C. | 132 | D. | 以上都不对 |
19.已知命题p:x2+2x-3>0,命题q:x>a,若¬q的一个充分不必要条件是¬p,则实数a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a≥-3 | D. | a>-3 |
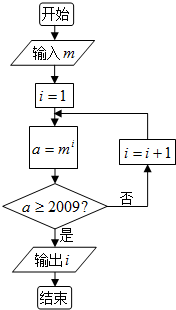 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)