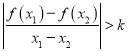题目内容
【题目】已知函数f(x)＝|x－a|．
(1)若不等式f(x)≤3的解集为{x|－1≤x≤5}，求实数a的值；
(2)在(1)的条件下，若f(x)＋f(x＋5)≥m对一切实数x恒成立，求实数m的取值范围．
【答案】（1）
；（2）
【解析】试题分析：（1）由|x-a|≤3 得a-3≤x≤a+3,再根据f（x）≤3的解集为[-1,5] 可得
,所以a=2．
（2）由|x-2|+|x+3|≥|（x-2）-（x+3）|=5可得m≤5．
试题解析：（1）∵|x-a|≤3 ，∴a-3≤x≤a+3，
∵f（x）≤3的解集为[-1,5] ，∴，∴a=2． 5分
（2）∵f（x）+f（x+5）=|x-2|+|x+3|≥|（x-2）-（x+3）|=5
又f（x）+f（x+5）≥m恒成立 ,∴m≤5． 10分
练习册系列答案
相关题目
【题目】某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球，再从装有1个蓝球与2个白球的袋中任意摸出1个球，根据摸出4个球中红球与蓝球的个数，设一、二、三等奖如下：
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级．
（1）求一次摸奖恰好摸到1个红球的概率；
（2）求摸奖者在一次摸奖中获奖金额X的分布列．