题目内容
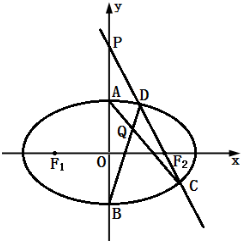
2.如图,已知F1、F2分别为椭圆 $\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1(a>b>0)的左、右焦点,其离心率e=$\frac{1}{2}$.且a+c=3,(1)求椭圆的标准方程;
(2)设A、B分别为椭圆的上下顶点,O为原点,过F2作直线l与椭圆交于C、D两点,并与y轴交于点P(异于A、B、O点),直线AC与直线BD交于点Q.则$\overrightarrow{OP}•\overrightarrow{OQ}$是否为定值,若是,请证明你的结论;若不是,请说明理由.
分析 (1)由离心率e=$\frac{c}{a}$=$\frac{1}{2}$,且a+c=3,又b2=a2-c2,联立解出即可.
(2)$\overrightarrow{OP}•\overrightarrow{OQ}$为定值3.当直线l垂直于x轴时,直接验证.当直线l不垂直于x轴时,设直线CD:my=x-1,C(x1,y1),D(x2,y2),P(0,-$\frac{1}{m}$),与椭圆方程联立可得:(3m2+4)y2+6m2y-9=0,由直线AC与BD的方程联立可得Q的纵坐标.再利用数量积运算及其根与系数的关系即可得出.
解答 解:(1)∵离心率e=$\frac{c}{a}$=$\frac{1}{2}$,且a+c=3,解得a=2,c=1.
又b2=a2-c2=3.
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)$\overrightarrow{OP}•\overrightarrow{OQ}$为定值3.当直线l垂直于x轴时,不符合题意,舍去.
当直线l不垂直于x轴时,设直线CD:my=x-1,C(x1,y1),D(x2,y2),P(0,-$\frac{1}{m}$).
联立.$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为(3m2+4)y2+6m2y-9=0,
∴y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$.直
线AC的方程为:$y-\sqrt{3}=\frac{{y}_{1}-\sqrt{3}}{{x}_{1}}x$,直线BD的方程为:$y+\sqrt{3}=\frac{{y}_{2}+\sqrt{3}}{{x}_{2}}x$.
消去x可得$\frac{y-\sqrt{3}}{y+\sqrt{3}}$=$\frac{{x}_{2}({y}_{1}-\sqrt{3})}{{x}_{1}({y}_{2}-\sqrt{3})}$,
∴$(\frac{y-\sqrt{3}}{y+\sqrt{3}})^{2}$=$\frac{{x}_{2}^{2}({y}_{1}-\sqrt{3})^{2}}{{x}_{1}^{2}({y}_{2}-\sqrt{3})^{2}}$=$\frac{(3-{y}_{2}^{2})({y}_{1}-\sqrt{3})^{2}}{(3-{y}_{1}^{2})({y}_{2}-\sqrt{3})^{2}}$=$\frac{({y}_{1}-\sqrt{3})({y}_{2}-\sqrt{3})}{({y}_{1}+\sqrt{3})({y}_{2}+\sqrt{3})}$=$\frac{{y}_{1}{y}_{2}-\sqrt{3}({y}_{1}+{y}_{2})+3}{{y}_{1}{y}_{2}+\sqrt{3}({y}_{1}+{y}_{2})+3}$=$\frac{\frac{-9}{3{m}^{2}+4}+\frac{6\sqrt{3}m}{3{m}^{2}+4}+3}{\frac{-9}{3{m}^{2}+4}-\frac{6\sqrt{3}m}{3{m}^{2}+4}+3}$=$(\frac{\sqrt{3}m+1}{\sqrt{3}m-1})^{2}$,
∵$-\sqrt{3}<{y}_{1},{y}_{2}<\sqrt{3}$,∴$\frac{y-\sqrt{3}}{y+\sqrt{3}}$与$\frac{{x}_{2}}{{x}_{1}}$异号,
${x}_{1}{x}_{2}={m}^{2}{y}_{1}{y}_{2}+m({y}_{1}+{y}_{2})+1$=${m}^{2}(-\frac{9}{3{m}^{2}+4})$+m$(-\frac{6m}{3{m}^{2}+4})$+1=$\frac{4(1-\sqrt{3}m)(1+\sqrt{3}m)}{3{m}^{2}+4}$,
∴$\frac{{x}_{2}}{{x}_{1}}$与$\frac{\sqrt{3}m+1}{\sqrt{3}m-1}$异号,
∴$\frac{y-\sqrt{3}}{y+\sqrt{3}}$与$\frac{\sqrt{3}m+1}{\sqrt{3}m-1}$同号,
∴$\frac{y-\sqrt{3}}{y+\sqrt{3}}$=$\frac{\sqrt{3}m+1}{\sqrt{3}m-1}$,解得y=-3m,
因此点Q(xQ,-3m),
∴$\overrightarrow{OP}•\overrightarrow{OQ}$=0-3m×$(-\frac{1}{m})$=3.
为定值3.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数的关系、数量积运算性质、直线的交点,考查了分类讨论方法、推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | 2-3i | B. | 2+3i | C. | 3+2i | D. | 3-2i |
| A. | 最小值为0,无最大值 | B. | 最小值为0,最大值为6 | ||
| C. | 最小值为-$\frac{1}{4}$,无最大值 | D. | 最小值为-$\frac{1}{4}$,最大值为6 |