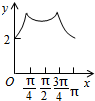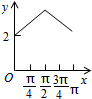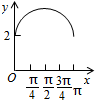题目内容
12.若x∈R,则函数f(x)=3-3sinx-cos2x的最大值,最小值分别为( )| A. | 最小值为0,无最大值 | B. | 最小值为0,最大值为6 | ||
| C. | 最小值为-$\frac{1}{4}$,无最大值 | D. | 最小值为-$\frac{1}{4}$,最大值为6 |
分析 由条件利用同角三角函数的基本关系求得f(x)=${(sinx-\frac{3}{2})}^{2}$-$\frac{1}{4}$,结合sinx∈[-1,1],利用二次函数的性质求得函数的最值.
解答 解:∵函数f(x)=3-3sinx-cos2x=sin2x-3sinx+2=${(sinx-\frac{3}{2})}^{2}$-$\frac{1}{4}$,sinx∈[-1,1],
∴当sinx=-1时,函数取得最大值为 6,当sinx=1时,函数取得最小值为0,
故选:B.
点评 本题主要考查同角三角函数的基本关系,二次函数的性质,正弦函数的值域,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
17.下列双曲线中,焦点在y轴上且渐近线方程为y=±2x的是( )
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-y2=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-$\frac{{x}^{2}}{4}$=1 |
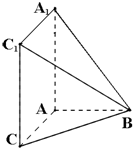 如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
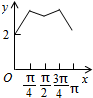
如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.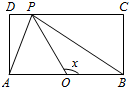 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )