题目内容

13．在平面直角坐标系xOy中，若直线y=2a与函数y=|x-a|-1的图象只有一个交点，则a的值为$-\frac{1}{2}$．

分析 由已知直线y=2a与函数y=|x-a|-1的图象特点分析一个交点时，两个图象的位置，确定a．

解答 解：由已知直线y=2a是平行于x轴的直线，由于y=x-a为一次函数，其绝对值的函数为对称图形，故函数y=|x-a|-1的图象是折线，所以直线y=2a过折线顶点时满足题意，
所以2a=-1，解得a=-$\frac{1}{2}$；
故答案为：$-\frac{1}{2}$．

点评 本题考查了函数的图象；考查利用数形结合求参数．

练习册系列答案
相关题目
3．设函数f（x）=$\left\{\begin{array}{l}{3x-1，}&{x＜1}\\{{2}^{x}，}&{x≥1}\end{array}\right.$，则满足f（f（a））=2f（a）的a的取值范围是（　　）
A．[$\frac{2}{3}$，1]B．[0，1]C．[$\frac{2}{3}$，+∞）D．[1，+∞）
4．圆心为（1，1）且过原点的圆的方程是（　　）
A．（x-1）2+（y-1）2=1B．（x+1）2+（y+1）2=1C．（x+1）2+（y+1）2=2D．（x-1）2+（y-1）2=2
1．已知集合A={-2，-1，0，1，2}，B={x|（x-1）（x+2）＜0}，则A∩B=（　　）
A．{-1，0}B．{0，1}C．{-1，0，1}D．{0，1，2}
8．设p：x＜3，q：-1＜x＜3，则p是q成立的（　　）
A．充分必要条件B．充分不必要条件
C．必要不充分条件D．既不充分也不必要条件
18．设函数f（x）=ln（1+x）-ln（1-x），则f（x）是（　　）
A．奇函数，且在（0，1）上是增函数B．奇函数，且在（0，1）上是减函数
C．偶函数，且在（0，1）上是增函数D．偶函数，且在（0，1）上是减函数
5．设F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点．若C上存在点P，使线段PF的中点恰为其虚轴的一个端点，则C的离心率为$\sqrt{5}$．
2．如图，已知F1、F2分别为椭圆 $\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1（a＞b＞0）的左、右焦点，其离心率e=$\frac{1}{2}$．且a+c=3，
（1）求椭圆的标准方程；
（2）设A、B分别为椭圆的上下顶点，O为原点，过F2作直线l与椭圆交于C、D两点，并与y轴交于点P（异于A、B、O点），直线AC与直线BD交于点Q．则$\overrightarrow{OP}•\overrightarrow{OQ}$是否为定值，若是，请证明你的结论；若不是，请说明理由．
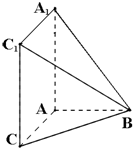3．如图，在四棱锥B-AA1C1C中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求二面角A1-BC1-C的余弦值； 
（Ⅲ）证明：在线段上BC1存在点D，使得AD⊥A1B，并求$\frac{BD}{B{C}_{1}}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网