题目内容

14．已知sin（α-β）cosα-cos（β-α）sinα=$\frac{3}{5}$，β是第三象限角，则tan（β+$\frac{π}{4}$）=7．

分析 利用两角和差的正弦公式进行化简，然后利用两角和差的正切公式进行计算即可．

解答 解：由sin（α-β）cosα-cos（β-α）sinα=$\frac{3}{5}$，
得sin（α-β-α）=sin（-β）=$\frac{3}{5}$，
∴sinβ=-$\frac{3}{5}$，
∵β是第三象限角，
∴cosβ=-$\frac{4}{5}$，tanβ=$\frac{3}{4}$，
则tan（β+$\frac{π}{4}$）=$\frac{tanβ+1}{1-tanβ}$=$\frac{\frac{3}{4}+1}{1-\frac{3}{4}}$=7，
故答案为：7；

点评 本题主要考查三角函数值的计算，利用两角和差的正弦公式和正切公式是解决本题的关键．

练习册系列答案
相关题目
4．圆心为（1，1）且过原点的圆的方程是（　　）
A．（x-1）2+（y-1）2=1B．（x+1）2+（y+1）2=1C．（x+1）2+（y+1）2=2D．（x-1）2+（y-1）2=2
5．设F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点．若C上存在点P，使线段PF的中点恰为其虚轴的一个端点，则C的离心率为$\sqrt{5}$．
2．如图，已知F1、F2分别为椭圆 $\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1（a＞b＞0）的左、右焦点，其离心率e=$\frac{1}{2}$．且a+c=3，
（1）求椭圆的标准方程；
（2）设A、B分别为椭圆的上下顶点，O为原点，过F2作直线l与椭圆交于C、D两点，并与y轴交于点P（异于A、B、O点），直线AC与直线BD交于点Q．则$\overrightarrow{OP}•\overrightarrow{OQ}$是否为定值，若是，请证明你的结论；若不是，请说明理由．
9．利用图象解不等式：-1＜tan2x≤$\sqrt{3}$．
19．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为 $\frac{{\sqrt{2}}}{2}$，其左、右焦点分别是F1，F2，过点F1的直线l交椭圆C于E，G两点，且△EGF2的周长为4$\sqrt{2}$
（Ⅰ）求椭圆C的方程；     
（Ⅱ）若过点M（2，0）的直线与椭圆C相交于两点A，B，设P为椭圆上一点，且满足 $\overrightarrow{OA}+\overrightarrow{OB}=t\overrightarrow{OP}$（O为坐标原点），当$|{\overrightarrow{PA}-\overrightarrow{PB}}|＜\frac{{2\sqrt{5}}}{3}$时，求实数t的取值范围．
6．乒乓球比赛用球的直径为40.00mm，一种乒乓球筒高200mm，现有4个乒乓球筒，要将5个比赛用球放到4个乒乓球筒里（乒乓球筒可以空着），共有多少种不同的放法？
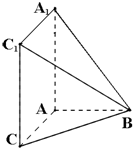3．如图，在四棱锥B-AA1C1C中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求二面角A1-BC1-C的余弦值； 
（Ⅲ）证明：在线段上BC1存在点D，使得AD⊥A1B，并求$\frac{BD}{B{C}_{1}}$的值．
4．设函数f（x）=x2-ax+b．
（Ⅰ）讨论函数f（sinx）在（-$\frac{π}{2}$，$\frac{π}{2}$）内的单调性并判断有无极值，有极值时求出最值；
（Ⅱ）记f0（x）=x2-a0x+b0，求函数|f（sinx）-f0（sinx）|在[-$\frac{π}{2}$，$\frac{π}{2}$]上的最大值D；
（Ⅲ）在（Ⅱ）中，取a0=b0=0，求z=b-$\frac{{a}^{2}}{4}$满足条件D≤1时的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网