题目内容
将正整数12分解成两个正整数的乘积有：1×12，2×6，3×4三种，其中3×4是这三种分解中两数差的绝对值最小的，我们称3×4为12的最佳分解，当p×q（p≤q且p、q∈N*）是正整数n的最佳分解时，我们规定函数f（n）=
，例如f（12）=
，关于函数f（n）有下列叙述：
①f（1）=
②f（24）=
③f（28）=
④f（144）=
其中正确的序号为______（填入所有正确的序号）．
| p |
| q |
| 3 |
| 4 |
①f（1）=
| 1 |
| 7 |
②f（24）=
| 3 |
| 8 |
③f（28）=
| 4 |
| 7 |
④f（144）=
| 9 |
| 16 |
其中正确的序号为______（填入所有正确的序号）．
对于①，因为7=1×7； 所以f(7)=
，故①对
对于②，因为24=1×24； 24=2×12； 24=3×8； 24=4×6所以f（24）=
故②错
对于③，因为28=1×28，28=2×14，28=4×7，所以f（28）=
故③对；
对于④因为144=1×144，144=2×72，144=3×48，144=12×12，144=9×16所以f（144）=1故④错．
故答案为：①③．
| 1 |
| 7 |
对于②，因为24=1×24； 24=2×12； 24=3×8； 24=4×6所以f（24）=
| 4 |
| 6 |
对于③，因为28=1×28，28=2×14，28=4×7，所以f（28）=
| 4 |
| 7 |
对于④因为144=1×144，144=2×72，144=3×48，144=12×12，144=9×16所以f（144）=1故④错．
故答案为：①③．
练习册系列答案
名题金卷系列答案
相关题目
，
，
，
，
，
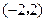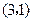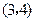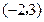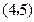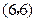为报刊零售点.请确定一个格点（除零售点外）__________为发行站，使6个零售点沿街道到发行站之间路程的和最短.
