题目内容
(本小题满分14分)
设函数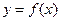 在
在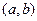 上的导函数为
上的导函数为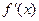 ,
,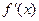 在
在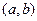 上的导函数为
上的导函数为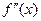 ,若在
,若在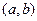 上,
上,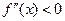 恒成立,则称函数
恒成立,则称函数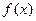 在
在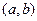 上为“凸函数”.已知
上为“凸函数”.已知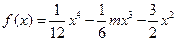 .
.
(1)若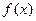 为区间
为区间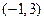 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数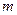 的值;
的值;
(2)若当实数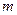 满足
满足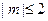 时,函数
时,函数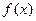 在
在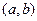 上总为“凸函数”,求
上总为“凸函数”,求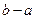 的最大值.
的最大值.
设函数
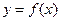 在
在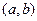 上的导函数为
上的导函数为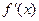 ,
,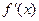 在
在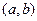 上的导函数为
上的导函数为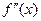 ,若在
,若在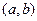 上,
上,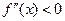 恒成立,则称函数
恒成立,则称函数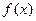 在
在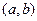 上为“凸函数”.已知
上为“凸函数”.已知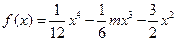 .
.(1)若
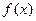 为区间
为区间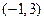 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数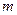 的值;
的值;(2)若当实数
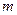 满足
满足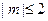 时,函数
时,函数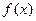 在
在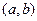 上总为“凸函数”,求
上总为“凸函数”,求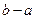 的最大值.
的最大值.解:由函数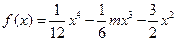 得,
得,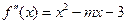 …………3分
…………3分
(Ⅰ) 若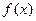 为区间
为区间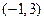 上的“凸函数”,则有
上的“凸函数”,则有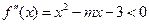 在区间
在区间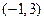 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当
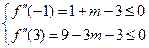 ,
,
即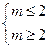
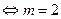 . …………………………………………………7分
. …………………………………………………7分
(Ⅱ)当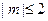 时,
时,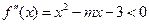 恒成立
恒成立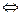 当
当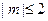 时,
时,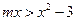 恒成立.…………………8分
恒成立.…………………8分
当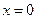 时,
时,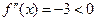 显然成立。 ………………………9分
显然成立。 ………………………9分
当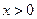 ,
,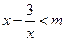
∵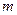 的最小值是
的最小值是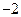 .
.
∴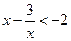 .
.
从而解得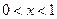 ……………………………………11分
……………………………………11分
当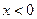 ,
,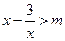
∵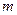 的最大值是
的最大值是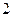 ,∴
,∴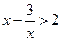 ,
,
从而解得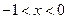 . ……………………………13分
. ……………………………13分
综上可得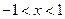 ,从而
,从而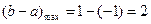 ……………14分
……………14分
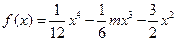 得,
得,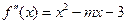 …………3分
…………3分(Ⅰ) 若
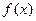 为区间
为区间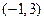 上的“凸函数”,则有
上的“凸函数”,则有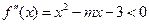 在区间
在区间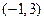 上恒成立,由二次函数的图像,当且仅当
上恒成立,由二次函数的图像,当且仅当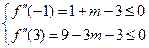 ,
,即
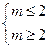
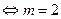 . …………………………………………………7分
. …………………………………………………7分(Ⅱ)当
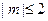 时,
时,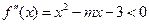 恒成立
恒成立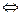 当
当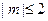 时,
时,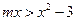 恒成立.…………………8分
恒成立.…………………8分当
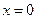 时,
时,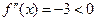 显然成立。 ………………………9分
显然成立。 ………………………9分当
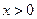 ,
,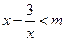
∵
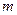 的最小值是
的最小值是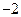 .
.∴
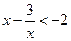 .
.从而解得
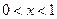 ……………………………………11分
……………………………………11分当
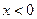 ,
,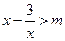
∵
 的最大值是
的最大值是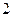 ,∴
,∴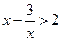 ,
,从而解得
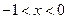 . ……………………………13分
. ……………………………13分综上可得
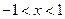 ,从而
,从而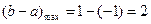 ……………14分
……………14分略

练习册系列答案
相关题目
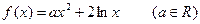 ,设曲线
,设曲线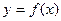 在点
在点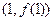 处的切线为
处的切线为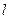 ,若
,若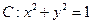 相切,求
相切,求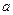 的值.
的值.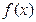 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: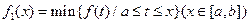 ,
,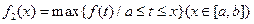 ,其中
,其中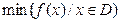 表示函数
表示函数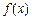 在D上的最小值,
在D上的最小值,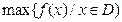 表示函数
表示函数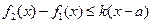 对任意的
对任意的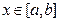 成立,则称函数
成立,则称函数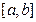 上的“k阶收缩函数”
上的“k阶收缩函数”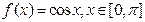 ,试写出
,试写出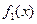 ,
, 的表达式;
的表达式;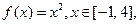 试判断
试判断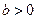 ,函数
,函数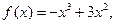 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围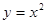 在
在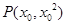 处的切线的倾斜角为
处的切线的倾斜角为 ,则点
,则点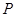 的坐标是( )
的坐标是( )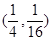
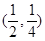
 一个对称图形做的薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻该薄片露出水面部分的图形面积为
一个对称图形做的薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻该薄片露出水面部分的图形面积为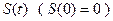 ,那么导函数
,那么导函数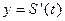 的图像大致为
的图像大致为

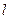 与曲线
与曲线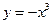 相切于点A(-1,1),则切线的方程是
相切于点A(-1,1),则切线的方程是 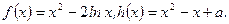
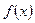 的极值;
的极值;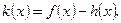 若函数
若函数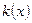 在
在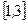 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数 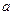 的取值范围.
的取值范围. 线
线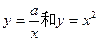 在它们的交点处的两条切线互相垂直,则
在它们的交点处的两条切线互相垂直,则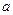 的值是 .
的值是 .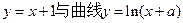 相切,则a的值为( )
相切,则a的值为( )