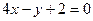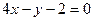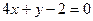题目内容
(本小题14分)
已知函数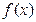 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义:
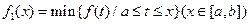 ,
,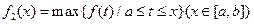 ,其中
,其中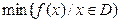 表示函数
表示函数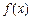 在D上的最小值,
在D上的最小值,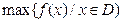 表示函数
表示函数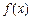 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得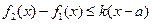 对任意的
对任意的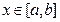 成立,则称函数
成立,则称函数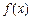 为
为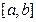 上的“k阶收缩函数”
上的“k阶收缩函数”
(1)若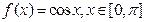 ,试写出
,试写出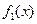 ,
,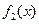 的表达式;
的表达式;
(2)已知函数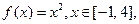 试判断
试判断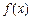 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,
如果是,求出对应的k,如果不是,请说明理由;
已知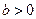 ,函数
,函数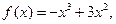 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围
已知函数
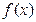 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: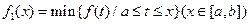 ,
,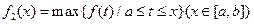 ,其中
,其中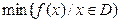 表示函数
表示函数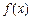 在D上的最小值,
在D上的最小值,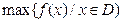 表示函数
表示函数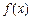 在D上的最大值,若存在最小正整数k,使得
在D上的最大值,若存在最小正整数k,使得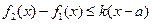 对任意的
对任意的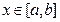 成立,则称函数
成立,则称函数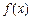 为
为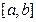 上的“k阶收缩函数”
上的“k阶收缩函数”(1)若
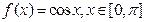 ,试写出
,试写出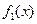 ,
,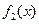 的表达式;
的表达式;(2)已知函数
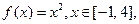 试判断
试判断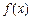 是否为[-1,4]上的“k阶收缩函数”,
是否为[-1,4]上的“k阶收缩函数”,如果是,求出对应的k,如果不是,请说明理由;
已知
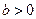 ,函数
,函数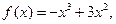 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围解:(1)由题意可得:
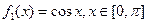 ,
,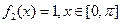 。
。(2)
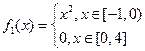 ,
,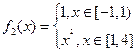 ,
,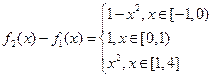
当
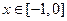 时,
时,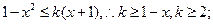
当
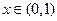 时,
时,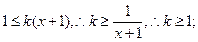
当
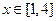 时,
时,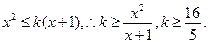
综上所述,
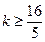 。
。即存在
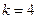 ,使得
,使得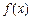 是[-1,4]上的“4阶收缩函数”。
是[-1,4]上的“4阶收缩函数”。(3)
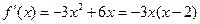 ,令
,令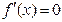 得
得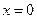 或
或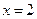 。
。函数
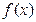 的变化情况如下:
的变化情况如下:| x | 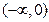 | 0 | 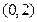 | 2 | 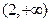 |
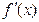 | - | 0 | + | 0 | - |
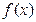 | 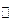 | 0 | 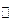 | 4 | 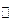 |
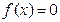 得
得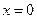 或
或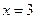 。
。(i)当
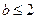 时,
时,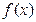 在
在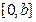 上单调递增,因此,
上单调递增,因此,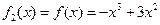 ,
,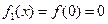 。因为
。因为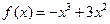 是
是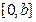 上的“二阶收缩函数”,所以,
上的“二阶收缩函数”,所以,①
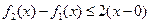 对
对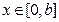 恒成立;
恒成立;②存在
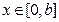 ,使得
,使得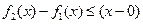 成立。
成立。①即:
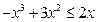 对
对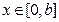 恒成立,由
恒成立,由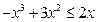 解得
解得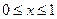 或
或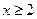 。
。要使
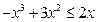 对
对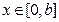 恒成立,需且只需
恒成立,需且只需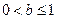 。
。②即:存在
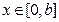 ,使得
,使得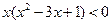 成立。
成立。由
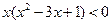 解得
解得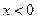 或
或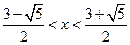 。
。所以,只需
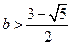 。
。综合①②可得
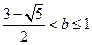 。
。(i i)当
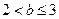 时,
时,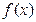 在
在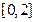 上单调递增,在
上单调递增,在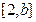 上单调递减,
上单调递减,因此,
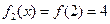 ,
,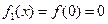 ,
,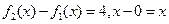 ,
,显然当
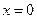 时,
时,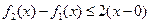 不成立。
不成立。(i i i)当
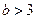 时,
时,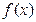 在
在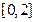 上单调递增,在
上单调递增,在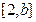 上单调递减,因此,
上单调递减,因此,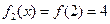 ,
,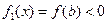 ,
,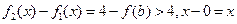 ,
,显然当
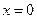 时,
时,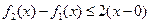 不成立。
不成立。综合(i)(i i)(i i i)可得:
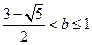
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
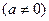 是R上的奇函数,
是R上的奇函数,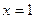 时
时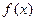 取得极值
取得极值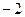 ,
,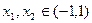 ,不等式
,不等式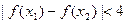 恒成立. 、
恒成立. 、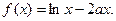
 处的切线为直线
处的切线为直线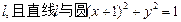 相切,求a的值;
相切,求a的值;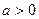 时,求函数
时,求函数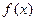 的单调区间。
的单调区间。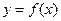 在
在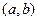 上的导函数为
上的导函数为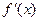 ,
,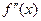 ,若在
,若在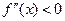 恒成立,则称函数
恒成立,则称函数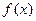 在
在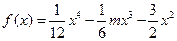 .
.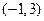 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数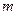 的值;
的值;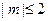 时,函数
时,函数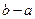 的最大值.
的最大值.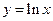 的切线,则切点为___________.
的切线,则切点为___________.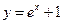 的图象在
的图象在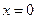 处的切线方程为
处的切线方程为 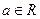 ,函数
,函数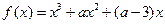 的导函数是
的导函数是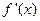 ,若
,若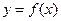 在原点处的切线方程为( )
在原点处的切线方程为( )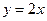
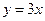

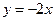
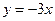
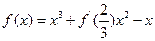 ,则函数
,则函数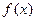 的图像在
的图像在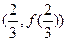 处的切线方程是
处的切线方程是  处的切线方程为( )
处的切线方程为( )