题目内容
已知等比数列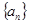 的首项
的首项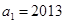 ,公比
,公比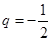 ,数列
,数列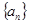 前
前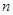 项的积记为
项的积记为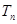 .
.
(1)求使得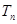 取得最大值时
取得最大值时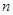 的值;
的值;
(2)证明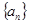 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为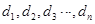 ,证明:数列
,证明:数列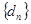 为等比数列.
为等比数列.
(参考数据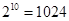 )
)
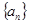 的首项
的首项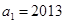 ,公比
,公比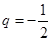 ,数列
,数列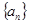 前
前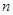 项的积记为
项的积记为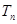 .
.(1)求使得
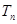 取得最大值时
取得最大值时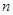 的值;
的值;(2)证明
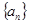 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为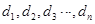 ,证明:数列
,证明:数列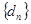 为等比数列.
为等比数列.(参考数据
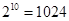 )
)(1)n=12
(2)根据题意,由于对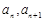 进行调整,
进行调整,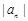 随n增大而减小,
随n增大而减小,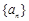 奇数项均正,偶数项均负,那么对于n分为奇数和偶数来讨论得到证明。
奇数项均正,偶数项均负,那么对于n分为奇数和偶数来讨论得到证明。
(2)根据题意,由于对
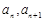 进行调整,
进行调整,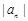 随n增大而减小,
随n增大而减小,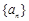 奇数项均正,偶数项均负,那么对于n分为奇数和偶数来讨论得到证明。
奇数项均正,偶数项均负,那么对于n分为奇数和偶数来讨论得到证明。试题分析:.解:
(1),
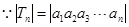 ,
,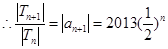 ,
,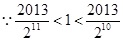 ,
,则当
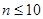 时,
时,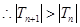 ;当
;当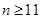 时,
时,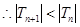 ,
,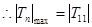 ,又
,又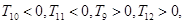
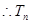 的最大值是
的最大值是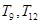 中的较大者.
中的较大者.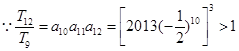 ,
,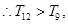 ,因此当n=12时,
,因此当n=12时,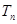 最大 .6分
最大 .6分(2)对
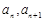 进行调整,
进行调整,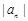 随n增大而减小,
随n增大而减小,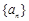 奇数项均正,偶数项均负.
奇数项均正,偶数项均负.①当n是奇数时,调整为
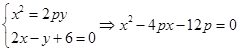 .则
.则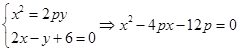 ,
,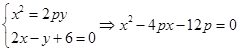 ,
,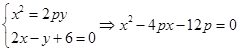 成等差数列;
成等差数列;②当n是偶数时,调整为
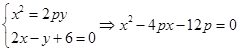 ;则
;则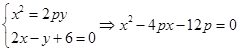 ,
,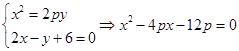 ,
,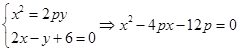 成等差数列;
成等差数列;综上可知,
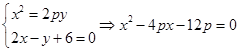 中的任意相邻三项按从小到大排列,总可以使其成等差数列.
中的任意相邻三项按从小到大排列,总可以使其成等差数列.①n是奇数时,公差
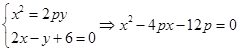 ;
;②n是偶数时,公差
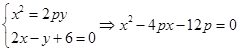 .
.无论n是奇数还是偶数,都有
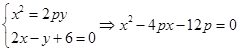 ,则
,则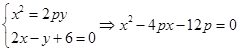 ,
,因此,数列
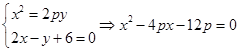 是首项为
是首项为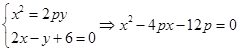 ,公比为
,公比为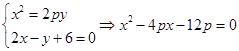 的等比数列,
的等比数列,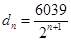 12分
12分点评:主要是考查了数列的概念的运用,以及分类讨论思想的运用,属于难度题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
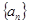 的前
的前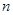 项和为
项和为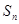 ,已知
,已知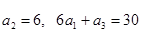 ,求
,求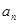 和
和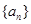 中,已知
中,已知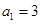 ,公比
,公比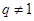 ,等差数列
,等差数列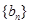 满足
满足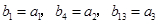 .
.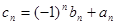 ,求数列
,求数列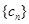 的前2n项和.
的前2n项和.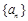 中,公比
中,公比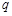 满足
满足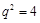 ,则
,则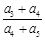 的值为 .
的值为 . 中,如果
中,如果
 ( )
( )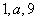 是等比数列,数列
是等比数列,数列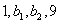 是等差数列,则
是等差数列,则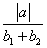 的值为 _____
的值为 _____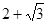 和
和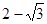 的等比中项是 ( )
的等比中项是 ( )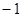
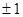
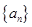 的前
的前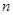 项和为
项和为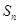 .已知
.已知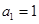 ,
,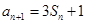 ,
,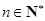 .
.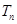 为数列
为数列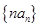 的前
的前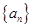 为等比数列,
为等比数列,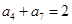 ,
,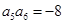 ,则
,则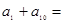 .
.