题目内容
在等比数列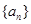 中,已知
中,已知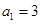 ,公比
,公比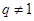 ,等差数列
,等差数列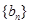 满足
满足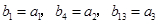 .
.
(Ⅰ)求数列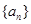 与
与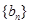 的通项公式;
的通项公式;
(Ⅱ)记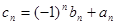 ,求数列
,求数列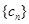 的前2n项和.
的前2n项和.
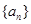 中,已知
中,已知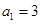 ,公比
,公比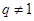 ,等差数列
,等差数列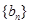 满足
满足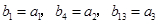 .
.(Ⅰ)求数列
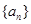 与
与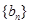 的通项公式;
的通项公式;(Ⅱ)记
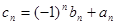 ,求数列
,求数列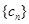 的前2n项和.
的前2n项和.(Ⅰ)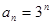 ,
,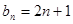 (Ⅱ)
(Ⅱ)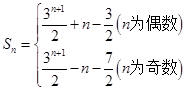
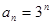 ,
,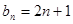 (Ⅱ)
(Ⅱ)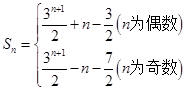
试题分析:(Ⅰ) 设等比数列
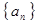 的公比为
的公比为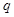 ,等差数列
,等差数列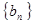 的公差为
的公差为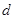 .
.由已知得:
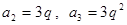 ,
, 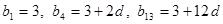
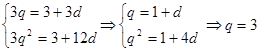 或
或 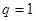 (舍去)
(舍去)所以, 此时
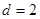
所以,
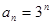 ,
, 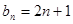 6分
6分 (2) 由题意
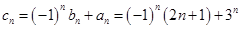
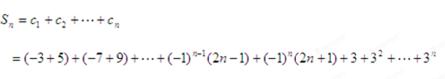
当n为偶数时:
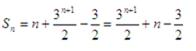
当n为奇数时:
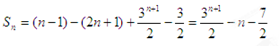
所以
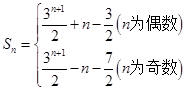
点评:等差数列通项
 ,等比数列通项
,等比数列通项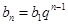 ,求通项公式主要需要找到首项公差公比,第二问数列
,求通项公式主要需要找到首项公差公比,第二问数列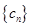 的通项由关于n的一次式与指数式相加构成的,因此采用分组求和法,这种方法以及裂项相消,错位相减等都是常用的求和方法
的通项由关于n的一次式与指数式相加构成的,因此采用分组求和法,这种方法以及裂项相消,错位相减等都是常用的求和方法
练习册系列答案
相关题目
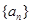 满足
满足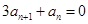 ,
,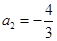 ,则
,则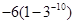
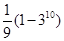
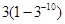
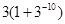
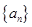 是首项为
是首项为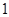 的等比数列,
的等比数列,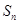 是
是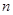 项和,且
项和,且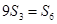 .则
.则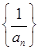 的前
的前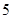 项和为.
项和为.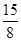 或
或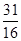 或
或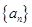 是公比为正数的等比数列,若
是公比为正数的等比数列,若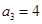 ,
,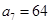 ,则
,则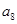 =( )
=( )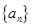 的前
的前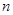 项和为
项和为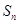 ,若
,若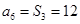 ,则
,则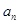 = .
= .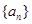 的各项均为正数,
的各项均为正数,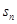 为其前
为其前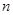 项和,对于任意的
项和,对于任意的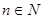 ,满足关系式
,满足关系式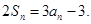
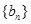 的通项公式是
的通项公式是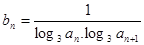 ,前
,前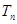 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有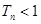
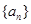 中,若
中,若 ,则
,则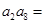 ( )
( )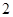

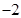
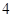
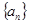 的首项
的首项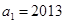 ,公比
,公比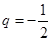 ,数列
,数列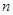 项的积记为
项的积记为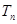 .
.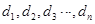 ,证明:数列
,证明:数列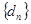 为等比数列.
为等比数列.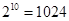 )
)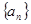 中,
中,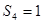 ,
,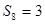 ,则
,则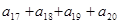 的值是( )
的值是( )