题目内容
18.(1)6男2女排成一排,2女相邻,有多少种不同的站法?(2)6男2女排成一排,2女不能相邻,有多少种不同的站法?
(3)4男4女排成一排,同性者相邻,有多少种不同的站法?
(4)4男4女排成一排,同性者不能相邻,有多少种不同的站法?
分析 (1)此题属于相邻问题,用“捆绑法”、以及分步计数原理求得结果.
(2)此题属于不相邻问题,用“插空法”求得结果.
(3)此题属于相邻问题,用“捆绑法”、以及分步计数原理求得结果.
(4)先把4个男的进行排列,方法有${A}_{4}^{4}$种,再把4个女的进行插空排列,方法有2${A}_{4}^{4}$种,再根据分布计数原理取得结果.
解答 解:(1)6男2女排成一排,2女相邻,先把2个女的:“绑在一起”,看成一个整体,方法有${A}_{2}^{2}$种,
再把此整体与其余的6个男的进行排列,方法有${A}_{7}^{7}$种,
再根据分步计数原理,所有的站法共有${A}_{2}^{2}$•${A}_{7}^{7}$=10080种方法.
(2)6男2女排成一排,2女不能相邻,先排6个男的,方法有${A}_{6}^{6}$种,再把2个女的插入6人形成的7个空中,
方法共有${A}_{7}^{2}$种,
再根据分步计数原理,所有的站法共有${A}_{6}^{6}$•${A}_{7}^{2}$=30240种方法.
(3)4男4女排成一排,同性者相邻,4个男的在一起排列,方法有${A}_{4}^{4}$种,再把4个女的在一起排列,方法有${A}_{4}^{4}$种,
再把这2个“整体”进行排列,故所有的排列数为 ${A}_{2}^{2}$•${A}_{4}^{4}$•${A}_{4}^{4}$=1152.
(4)4男4女排成一排,同性者不能相邻,先把4个男的进行排列,方法有${A}_{4}^{4}$种,再把4个女的进行插空排列,方法有2${A}_{4}^{4}$种,
故所有的排列方法共有2${A}_{4}^{4}$•${A}_{4}^{4}$=1152 种.
点评 本题主要考查排列组合问题,相邻问题用“捆绑法”,不相邻问题用“插空法”,属于中档题.

| A. | 2x+y+1=0 | B. | x+2y+2=0 | C. | x-2y-2=0 | D. | 2x-y-1=0 |
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
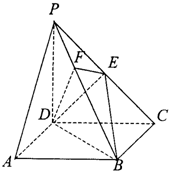 如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PD⊥底面ABCD,PD=AD,E为PC的中点,F为PB上一点,且EF⊥PB.