题目内容
9.到椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1左焦点的距离与到定直线x=2距离相等的动点轨迹方程是y2=-8x.分析 通过椭圆的左焦点及题意可知动点轨迹为抛物线,进而可得结论.
解答 解:椭圆$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1左焦点坐标为(-2,0),
由抛物线定义得:到左焦点(-2,0)的距离与到定直线x=2距离相等的动点轨迹是以(-2,0)为焦点,x=2为准线的抛物线,
∴动点轨迹方程是:y2=-8x,
故答案为:y2=-8x.
点评 本题考查求抛物线的方程,注意解题方法的积累,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.抛物线x2=4y的焦点到准线的距离为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
14.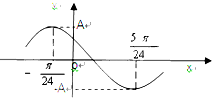 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其部分图象如下图所示,且直线y=A与曲线y=f(x)(-$\frac{π}{24}$$≤x≤\frac{11π}{24}$)所围成的封闭图形的面积为π,则f($\frac{π}{8}$)+f($\frac{2π}{8}$)+f($\frac{3π}{8}$)+…+f($\frac{2015π}{8})$的值为( )| A. | -$\sqrt{3}$ | B. | -1-$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -1+$\sqrt{3}$ |
1.过顶点在原点,焦点在y轴正半轴的抛物线的焦点F作直线l交抛物线于A、B两点,过点A、B分别作抛物线准线的垂线,垂足分别为点C、D,|AF|=2|BF|,且$\overrightarrow{DC}$•$\overrightarrow{BA}$=72,则该抛物线方程为( )
| A. | x2=8y | B. | x2=10y | C. | x2=9y | D. | x2=5y |
 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,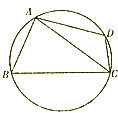 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.