题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点到焦点距离的最大值为$\sqrt{2}$+1,离心率为$\frac{{\sqrt{2}}}{2}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C交于A,B两点,设P为椭圆上一点,且满足$\overrightarrow{OA}$+$\overrightarrow{OB}$=t$\overrightarrow{OP}$(O为坐标原点),当|$\overrightarrow{PA}$-$\overrightarrow{PB}$|<$\frac{2\sqrt{5}}{3}$时,求实数t的取值范围.
分析 (Ⅰ)由题意知$\left\{\begin{array}{l}{a+c=\sqrt{2}+1}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\end{array}\right.$,可得a、c的值,从而可得b2的值,代入椭圆的方程可得答案;
(Ⅱ)由题意分析可知,直线AB的斜率存在,从而设AB的方程为y=k(x-2),设A(x1,y1)B(x2,y2);联立直线与椭圆的方程,可得(1+2k2)x2-8k2x+8k2-2=0,令△>0,解得k2的范围,由韦达定理,可得$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{8{k}^{2}}{1+2{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{8{k}^{2}-2}{1+2{k}^{2}}}\end{array}\right.$,又由$\overrightarrow{OA}$+$\overrightarrow{OB}$=t$\overrightarrow{OP}$,可得得(x1+x2,y1+y2,)=t(x,y);由此可以表示x以及y,由于点P在椭圆上,代入椭圆方程化简可得16k2=t2(1+2k2),又由|$\overrightarrow{PA}$-$\overrightarrow{PB}$|<$\frac{2\sqrt{5}}{3}$,可得$\sqrt{1+{k}^{2}}$|x1-x2|<$\frac{2\sqrt{5}}{5}$,结合t与k的关系式,变形可得可得关于t的不等式,解可得答案.
解答 解:(Ⅰ)由题意知$\left\{\begin{array}{l}{a+c=\sqrt{2}+1}\\{\frac{c}{a}=\frac{\sqrt{2}}{2}}\end{array}\right.$,可得a=$\sqrt{2}$,c=1;
从而b2=a2-c2=1,
所以椭圆C的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)由题意知,直线AB的斜率存在,
设AB的方程为y=k(x-2),A(x1,y1)B(x2,y2);
由$\left\{\begin{array}{l}{y=k(x-2)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(1+2k2)x2-8k2x+8k2-2=0,
根据条件可知△=(8k2)2-4(1+2k2)(8k2-2)>0,解得k2<$\frac{1}{2}$,
由韦达定理,可得$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{8{k}^{2}}{1+2{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{8{k}^{2}-2}{1+2{k}^{2}}}\end{array}\right.$,
又由$\overrightarrow{OA}$+$\overrightarrow{OB}$=t$\overrightarrow{OP}$,得(x1+x2,y1+y2,)=t(x,y);
所以$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}}{t}=\frac{8{k}^{2}}{t(1+2{k}^{2})}}\\{y=\frac{{y}_{1}+{y}_{2}}{t}=\frac{-4k}{t(1+2{k}^{2})}}\end{array}\right.$,
点P在椭圆上,得[$\frac{8{k}^{2}}{t(1+2{k}^{2})}$]2+2[$\frac{-4k}{t(1+2{k}^{2})}$]2=2,化简可得16k2=t2(1+2k2),即t2=$\frac{16{k}^{2}}{1+2{k}^{2}}$,
又由|$\overrightarrow{PA}$-$\overrightarrow{PB}$|<$\frac{2\sqrt{5}}{3}$,得$\sqrt{1+{k}^{2}}$|x1-x2|<$\frac{2\sqrt{5}}{5}$,即得$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$<$\frac{2\sqrt{5}}{5}$,
变形可得,(1+k2)[$\frac{64{k}^{4}}{(1+2{k}^{2})^{2}}$-4×$\frac{8{k}^{2}-2}{1+2{k}^{2}}$]<$\frac{20}{9}$,
化简可得(4k2-1)(14k2+13)>0,
解可得k2>$\frac{1}{4}$,所以$\frac{1}{4}$<k2<$\frac{1}{2}$
,而t2=$\frac{16{k}^{2}}{1+2{k}^{2}}$=8-$\frac{8}{1+2{k}^{2}}$,得$\frac{8}{3}$<8-$\frac{8}{1+2{k}^{2}}$<4,
解可得-2<t<-$\frac{2\sqrt{6}}{3}$或$\frac{2\sqrt{6}}{3}$<t<2,
所以实数t的范围为(-2,-$\frac{2\sqrt{6}}{3}$)∪($\frac{2\sqrt{6}}{3}$,2).
点评 本题考查直线与圆锥曲线方程的综合运用,解题时一般要联立直线与圆锥曲线的方程,根据题意,结合韦达定理进行计算分析.

 名校课堂系列答案
名校课堂系列答案| A. | (-1,1) | B. | (-1,-1) | C. | (1,-1) | D. | (1,1) |
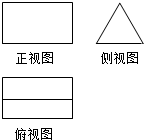
| A. | 棱锥 | B. | 棱台 | C. | 圆锥 | D. | 棱柱 |