题目内容
19．某公园设计节日鲜花摆放方案中一个花坛，其中一个花坛由一批花盆堆成六角垛．顶层一个，以下各层堆成正六边形，逐层每边增加一个花盆，设第n层共有花盆的个数为f（n），则f（n）的表达式为f（n）=3n（n-1）+1．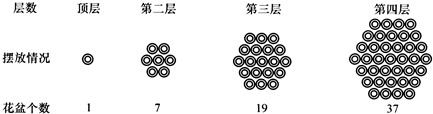
分析 由题意可得f（2）-f（1）=6，f（3）-f（2）=12，f（4）-f（3）=18，…，f（n）-f（n-1）=6（n-1）；从而解得．
解答 解：由图可知，
f（1）=1，f（2）=7，f（3）=19，f（4）=37；
故f（2）-f（1）=6，
f（3）-f（2）=12，
f（4）-f（3）=18，
…
f（n）-f（n-1）=6（n-1）；
相加得，f（n）-f（1）=6+12+18+…+6（n-1）；
故f（n）=3n（n-1）+1，
故答案为：f（n）=3n（n-1）+1．
点评 本题考查了归纳推理的应用，同时考查了叠加法的应用，属于基础题．
练习册系列答案
相关题目
9．阅读程序图，该程序图输出的结果是（ ）
| A． | 94 | B． | 92 | C． | 95 | D． | 93 |
10．
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则异面直线AC1与BB1所成的角的余弦值为（ ）
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=1，则异面直线AC1与BB1所成的角的余弦值为（ ）| A． | $\frac{2\sqrt{2}}{3}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |
17．已知直线y=kx+1与椭圆$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{m}$=1恒有公共点，则实数m的取值范围为（ ）
| A． | m≥1 | B． | m≥1或0＜m＜1 | C． | m≥1且m≠5 | D． | 0＜m＜5且m≠1 |