题目内容
6．已知梯形ABCD中，AD=DC=CB=$\frac{1}{2}$AB，P是BC边上一点，且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$，当P在BC边上运动时，x+y的最大值是$\frac{3}{2}$．分析 由条件利用两个向量的加减法的法则，以及其几何意义可得 $\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=（1-$\frac{λ}{2}$）$\overrightarrow{AB}$+λ$\overrightarrow{AD}$，λ∈[0，1]，再根据$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$，求得x、y 的值，可得x+y的最大值．
解答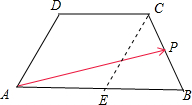 
解：设AB的中点为E，则由题意可得△BCE为等边三角形，且$\overrightarrow{BC}$=$\overrightarrow{EC}$-$\overrightarrow{EB}$=$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$，
再根据$\overrightarrow{BP}$、$\overrightarrow{BC}$共线，可得$\overrightarrow{BP}$=λ$\overrightarrow{BC}$=λ（$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$ ），λ∈[0，1]，
∴$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=（1-$\frac{λ}{2}$）$\overrightarrow{AB}$+λ$\overrightarrow{AD}$．
又$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$，∴$\left\{\begin{array}{l}{x=1-\frac{λ}{2}}\\{y=λ}\end{array}\right.$，∴x+y=1-$\frac{λ}{2}$+λ=1+$\frac{λ}{2}$≤1+$\frac{1}{2}$=$\frac{3}{2}$，
故x+y的最大值是$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题主要考查两个向量的加减法的法则，以及其几何意义，体现了数形结合的数学思想，属于基础题．
期末集结号系列答案| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{3}$或$\frac{2π}{3}$ |