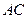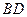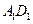题目内容
已知: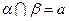 ,α⊥γ,β⊥γ,b∥α,b∥β.
,α⊥γ,β⊥γ,b∥α,b∥β.
求证:a⊥γ且b⊥γ.
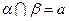 ,α⊥γ,β⊥γ,b∥α,b∥β.
,α⊥γ,β⊥γ,b∥α,b∥β.求证:a⊥γ且b⊥γ.
在a上任取一点P,过P作PQ⊥r.
∵β⊥r, ∴ ,
,
∵α⊥r, ∴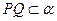 ,
,
∴PQ与a重合,故a⊥r.
过b和点P作平面S,
则S和α交于PQ1,S和β交于PQ2,
∵b∥α,b∥β
∴b∥PQ1,且b∥PQ2.
于是PQ1和PQ2与a重合,
故b∥a, 而a⊥r, ∴b⊥r.
∵β⊥r, ∴
 ,
,∵α⊥r, ∴
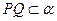 ,
,∴PQ与a重合,故a⊥r.
过b和点P作平面S,
则S和α交于PQ1,S和β交于PQ2,
∵b∥α,b∥β
∴b∥PQ1,且b∥PQ2.
于是PQ1和PQ2与a重合,
故b∥a, 而a⊥r, ∴b⊥r.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
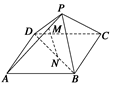
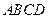 中,
中,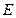 ,
,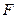 分别是
分别是 ,
,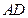 的中点.
的中点.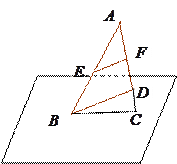 求证:
求证: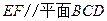
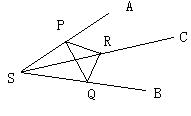
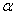 和共面的直线m、n,下列命题中真命题是 ( )
和共面的直线m、n,下列命题中真命题是 ( )
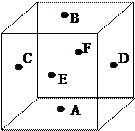
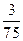
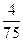


 中,若
中,若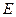 是
是 的中点,则直线
的中点,则直线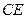 垂直于( )
垂直于( )