题目内容
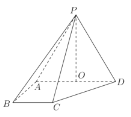
【题目】如图,已知四棱锥![]() ,
,![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
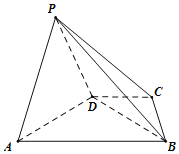
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,连接
,连接![]() ,先证明
,先证明![]() ,再证明
,再证明![]() 平面
平面![]() ,最后得出结论;
,最后得出结论;
(Ⅱ)分别延长![]() 交于
交于![]() ,过
,过![]() 作
作![]() 与点
与点![]() ,连接
,连接![]() ,
,![]() 为所求的二面角的平面角,在
为所求的二面角的平面角,在![]() 中,求出结果即可.
中,求出结果即可.
(Ⅰ)证明:取AD的中点O,连接PO,则![]() ,连接OC,
,连接OC,
在直角梯形ABCD中,易知![]() ,
,![]() ,
,![]() ,
,
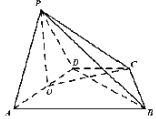
所以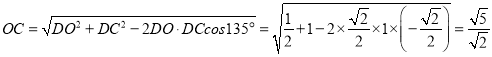 ,
,
由![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面ABCD,
平面ABCD,
又PO在平面PAD内,故平面![]() 平面ABCD;
平面ABCD;
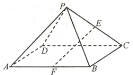
(Ⅱ)如图,分别延长![]() ,
,![]() 交于
交于![]() ,过
,过![]() 作
作![]() 与点
与点![]() ,连接
,连接![]() ,
,![]() ,
,
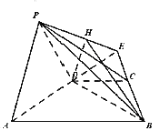
![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,由
,由![]() 平面
平面![]() 平面ABCD,
平面ABCD,
所以![]() 平面
平面![]() ,
,
结合(Ⅰ),则![]() 为所求的二面角的平面角,
为所求的二面角的平面角,![]() ,
,
由![]() ,
,
在三角形PDE中,由![]() ,
,![]() ,
,
所以![]() ,则
,则![]() ,
,
故平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某公司为了解某产品的获利情况,将今年1至7月份的销售收入![]() (单位:万元)与纯利润
(单位:万元)与纯利润![]() (单位:万元)的数据进行整理后,得到如下表格:
(单位:万元)的数据进行整理后,得到如下表格:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
的线性回归方程,再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
(1)求纯利润![]() 关于销售收入
关于销售收入![]() 的线性回归方程(精确到0.01);
的线性回归方程(精确到0.01);
(2)若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元,则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想?
参考公式:![]() ,
,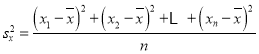 ,
,![]() ,
,![]() ;参考数据:
;参考数据:![]() .
.