题目内容
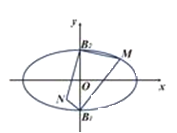
【题目】已知椭圆
的焦点
和
长轴长
.
（1）设直线
交椭圆于
两点，求线段
的中点坐标.
（2）求过点
的直线被椭圆所截弦的中点的轨迹方程.
【答案】（1）
（2）
，其中
【解析】
（1）根据焦点坐标得出椭圆的焦点在x轴上，由椭圆的焦点坐标得出c的值，再由长轴的值求出a的值，进而利用椭圆的性质求出b的值，确定出椭圆的标准方程，与直线y＝x+2联立，消去y得到关于x的一元二次方程，设出两交点A与B的坐标，利用根与系数的关系求出两根之和，即为两交点横坐标之和，利用中点坐标公式即可求出AB中点M的横坐标，代入直线方程可得M的纵坐标，进而确定出线段AB的中点坐标；
（2）设过点（0，2）的直线方程的斜率为k，表示出直线方程，与椭圆方程联立，消去y得到关于x的一元二次方程，由直线与椭圆有两个不同的交点，得到根的判别式大于0，列出关于k的不等式，求出不等式的解集得到k的范围，设出直线与椭圆的两交点坐标，利用韦达定理表示出两交点横坐标之和，利用中点坐标公式表示出线段AB中点C的横坐标，代入直线方程可得C的纵坐标，消去参数k即可得到所求的轨迹方程．
（1）由已知条件得椭圆的焦点在x轴上，其中
，从而
，
所以其标准方程是: 
联立方程组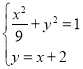
，消去
得,
设
线段中点为
那么
所以
也就是说线段
中点坐标为
（2）设直线方程为
把它代入
整理得: 
要使直线和椭圆有两个不同交点，则
，即
设直线与椭圆两个交点为
中点坐标为
，则
从参数方程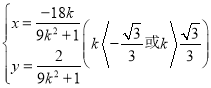
，
消去
得：，且
综上，所求轨迹方程为，其中
【题目】郑汴一体化是依托郑州省会城市资源优势发展开封的省级战略，实施至今，取得了一系列的成就：两城电信同价，金融同城，郑开大道全线贯通，城际列车实常态化运营．随着郑汴一体化的深入推进，很多人认为郑州开封未来有望合并．为了解市民对郑汴合并的态度，现随机抽查55人，结果按年龄分类统计形成如下表格：
支持 | 反对 | 合计 | |
不足35岁 | 20 | ||
35岁以上 | 30 | ||
合计 | 25 | 55 |
（1）请完成上面的2×2列联表，并判断是否有99.5%的把握认为市民对郑汴合并的态度与年龄有关？
（2）在上述样木中用分层抽样的方法，从攴持郑汴合并的两组市民中随机抽取6人作进一步调查，从这6人中任选2人，求恰有1位“不足35岁”的市民和1位“35岁及以上”的市民的概率．
附：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.814 | 5.024 | 7.879 | 10.828 |
