题目内容
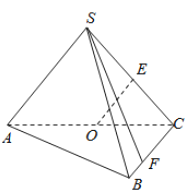
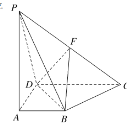
【题目】如图:四棱锥P-ABCD底面为一直角梯形,AB⊥AD,CD⊥AD,CD=2AB,PA⊥平面ABCD,F是PC中点。
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)求证:BF∥平面PAD。
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
(Ⅰ)由题意利用线面垂直的判定定理可证得![]() 平面
平面![]() ,然后利用线面垂直的判定定理证明题中的结论即可.
,然后利用线面垂直的判定定理证明题中的结论即可.
(Ⅱ)取 ![]() 的中点为
的中点为![]() ,连接
,连接![]() ,由几何关系可证得四边形
,由几何关系可证得四边形![]() 为平行四边形,据此有
为平行四边形,据此有![]() ,结合线面平行的判定定理即可证得题中的结论.
,结合线面平行的判定定理即可证得题中的结论.
(Ⅰ)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴ ![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)取 ![]() 的中点为
的中点为![]() ,连接
,连接![]()
∵ ![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中位线,
的中位线,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,并且
,并且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()