题目内容
【题目】设函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)设函数![]() ,若当
,若当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)在 上是增函数,在
上是增函数,在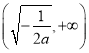 上是减函数;(2)
上是减函数;(2)![]()
【解析】
(1)求出定义域、![]() ,分
,分![]() ,
,![]() 两种情况进行讨论,通过解不等式
两种情况进行讨论,通过解不等式![]() ,
,![]() 可得单调区间;
可得单调区间;
(2)令![]() ,则
,则![]() ,则问题转化为当
,则问题转化为当![]() 时,
时,![]() 恒成立,进而转化求函数
恒成立,进而转化求函数![]() 的最大值问题.求导数
的最大值问题.求导数![]() ,根据极值点与区间
,根据极值点与区间![]() 的关系进行讨论可求得函数的最大值;
的关系进行讨论可求得函数的最大值;
(1)解:因为![]() ,其中
,其中![]() .所以
.所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上是增函数.
上是增函数.
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以![]() 在
在 上是增函数,在
上是增函数,在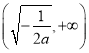 上是减函数.
上是减函数.
(2)令![]() ,则
,则![]() ,
,
根据题意,当![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() ,
,
①当![]() 时,
时,![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 不会恒成立,故不符题意.
不会恒成立,故不符题意.
②当![]() 时,
时,![]() 时,
时,![]() 恒成立.
恒成立.
所以![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 不会恒成立,故不符题意.
不会恒成立,故不符题意.
③当![]() 时,
时,![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是减函数,
上是减函数,
于是“![]() 对任意
对任意![]() 都成立”的充要条件是
都成立”的充要条件是![]() ,
,
即![]() ,解得
,解得![]() ,故
,故![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
【题目】已知z,y之间的一组数据如下表:
x | 1 | 3 | 6 | 7 | 8 |
y | 1 | 2 | 3 | 4 | 5 |
(1)从x ,y中各取一个数,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为![]() 与
与![]() ,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.