Question

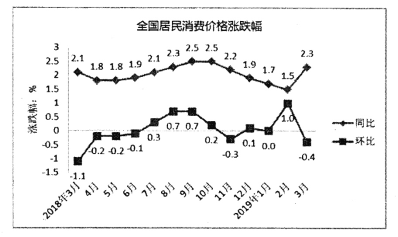
【题目】某工厂要建造一个长方体无盖贮水池，其容积为，深3m．如果池底每平方米的造价为200元，池壁每平方米的造价为150元，怎样设计水池能使总造价最低？最低总造价是多少？

Answer 1

【答案】将水池的底面设计成边长为20m的正方形时，总造价最低，最低总造价是116000元

【解析】

设出底面的长为,宽为,根据总容积求得与的等量关系.表示出总的造价后,将式子转化为关于的等式,结合基本不等式可求得最低总造价及底面的长和宽的值.

设底面的长为m,宽为m,水池总造价为元,

容积为1,可得,

因此,

根据题意, 池底每平方米的造价为200元,池壁每平方米的造价为150元,有

,

由基本不等式及不等式性质,可得

,

即,

当且仅当时,等号成立.

所以,将水池的底面设计成边长为20m的正方形时,总造价最低,最低总造价是116000元.