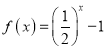题目内容
【题目】设函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集
的解集
(2)若函数![]() ,且
,且![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
(1)当![]() 时,不等式化为|x+2|<x2,去绝对值,解不等式即可;
时,不等式化为|x+2|<x2,去绝对值,解不等式即可;
(2)求出g(x)的最小值,使得所以g(x)min≤11即可.
(1)当a=2时,不等式化为|x+2|<x2,
所以-x2<x+2<x2,所以x>2或x<-1,
所以不等式的解集为:{x|x>2或x<-1}.
(2)方法一:g(x)=f(2x)+f(1-x)
=|2x+a|+|x-(a+1)|=|x+![]() |+|x+
|+|x+![]() |+|x-(a+1)|
|+|x-(a+1)|
≥|![]() +a+1|=|
+a+1|=|![]() +1|,
+1|,
因为g(x)≤11(a>0)有解,所以g(x)min≤11,即![]() ,
,
所以3a≤20,所以0<a![]() ,
,
所以a的取值范围为(0,![]() ];
];
方法二: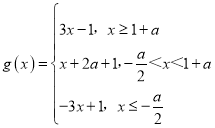 ,
,
当x=![]() 时,
时,![]() ,
,
因为g(x)≤11(a>0)有解,所以g(x)min≤11,即![]() ,
,
所以3a≤20,所以0<a![]() ,
,
所以a的取值范围为(0,![]() ].
].

【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
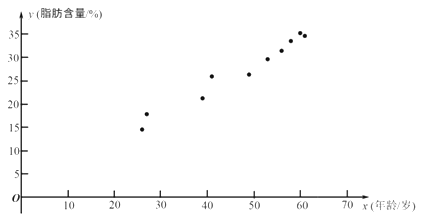
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:img src="http://thumb.zyjl.cn/Upload/2019/08/18/08/786210e5/SYS201908180802150104289801_ST/SYS201908180802150104289801_ST.007.png" width="51" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数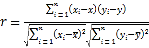
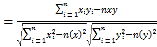
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为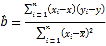 ,
,![]() .
.