题目内容
【题目】已知椭圆
：
的焦距为
，点
在椭圆上.
（1）求椭圆方程；
（2）设直线
：
与椭圆交于
，
两点，且直线
，
，
的斜率之和为0.
①求证：直线经过定点，并求出定点坐标；
②求
面积的最大值.
【答案】（1）
；（2）①证明见解析；②1
【解析】
(1)由条件有
，将点
代入椭圆方程结合
，可求解椭圆方程.
(2) ①设点
，
，设直线
，
，
的斜率分别为
，由条件有
，将直线方程与椭圆方程联立，将
，
代入化简可得
，得到直线过定点.
②由①利用弦长公式可求出
，再求出原点
到直线的距离，则
的面积可表示出来，从而可求其最大值.
解：（1）由题意可得，又由点在椭圆
上，故得
，
∵
，解得
，
.
∴椭圆的方程为；
（2）设点，.
联立
得
，
∴
，
化简得
①，
②，
③
设直线，，的斜率分别为
直线，，的斜率之和为0，∴
，
即
，
∴
，又
，∴.
综上可得，直线
经过定点
.
②由①知
.
∴
，
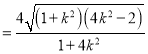原点到直线的距离
.
∴
，
∵
，
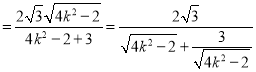当且仅当
，即
取“
”.
∴
，即面积的最大值为1.
练习册系列答案
相关题目
【题目】某集团公司为了加强企业管理，树立企业形象，考虑在公司内部对迟到现象进行处罚.现在员工中随机抽取200人进行调查，当不处罚时，有80人会迟到，处罚时，得到如下数据：
处罚金额 | 50 | 100 | 150 | 200 |
迟到的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
（Ⅰ）当处罚金定为100元时，员工迟到的概率会比不进行处罚时降低多少？
（Ⅱ）将选取的200人中会迟到的员工分为
，
两类：类员工在罚金不超过100元时就会改正行为；类是其他员工.现对类与类员工按分层抽样的方法抽取4人依次进行深度问卷，则前两位均为类员工的概率是多少？
