题目内容
【题目】某小学六年级学生的进行一分钟跳绳检测，现一班二班各有50人，根据检测结果绘出了一班的频数分布表和二班的频率分布直方图.
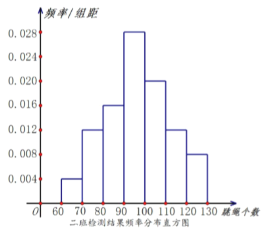
一班检测结果频数分布表：
跳绳个数区间 |
|
|
|
|
|
频数 | 7 | 13 | 20 | 8 | 2 |
（1）根据给出的图表估计一班和二班检测结果的中位数（结果保留两位小数）；
（2）跳绳个数不小于100个为优秀，填写下面2×2列联表，并根据列联表判断是否有95%的把握认为检测结果是否优秀与班级有关.
一班 | 二班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式及数据：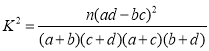
，
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【答案】（1）一班和二班检测结果的中位数分别为
，
；（2）列联表见解析，有95%的把握认为检测结果是否优秀与班级有关.
【解析】
（1）设一班中位数为m，由中位数两侧频数为25列出方程可得答案；
设二班中位数为n，由中位数两侧的频率相等且为
列方程可得n的值；
（2）补全2×2列联表，计算
的值，对照临界值表进行比较可得答案.
解：（1）设一班中位数为m，
则
,得
设二班中位数为n，则
，
得
.
（2）补全2×2列联表可得：
一班 | 二班 | 合计 | |
优秀 | 10 | 20 | 30 |
不优秀 | 40 | 30 | 70 |
合计 | 50 | 50 | 100 |
故
，
故有95%的把握认为检测结果与优秀与班级有关.
【题目】细叶青萎藤又称海风藤，俗称穿山龙，属木质藤本植物，是我国常用大宗中药材，以根茎入药，具有舒筋活血、祛风止痛、止咳平喘、强身健体等医疗保健功效.通过研究光照、温度和沙藏时间对细叶青萎藤种子萌发的影响，结果表明，细叶青萎藤种子发芽率和发芽指数均随着沙藏时间的延长而提高.
下表给岀了2019年种植的一批试验细叶青萎藤种子6组不同沙藏时间发芽的粒数.经计算：
沙藏时间 | 22 | 23 | 25 | 27 | 29 | 30 |
发芽数 | 8 | 11 | 20 | 30 | 59 | 70 |
，
，
，
.其中
，
分别为试验数据中的天数和发芽粒数，
.
（1）求
关于
的回归方程
（
和
都精确到0.01）；
（2）在题中的6组发芽的粒数不大于30的组数中，任意抽岀两组，则这两组数据中至少有一组满足“
”的概率是多少？
附：对于一组数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为：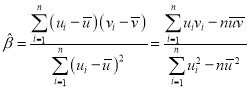
，
.
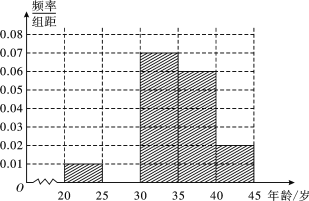
【题目】为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处．现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示．
分组（单位：岁） | 频数 | 频率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合计 |
|
|
（1）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图）,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数；
（2）在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望．
