题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.
(1)求椭圆C的方程;
(2)已知直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,是否存在实数k使得以线段
两点,是否存在实数k使得以线段![]() 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,当
;(2)存在,当![]() 时,以线段
时,以线段![]() 为直径的圆恰好经过坐标原点O.
为直径的圆恰好经过坐标原点O.
【解析】
(1)设椭圆的焦半距为![]() ,利用离心率为
,利用离心率为![]() ,椭圆
,椭圆![]() 的长轴长为4.列出方程组求解
的长轴长为4.列出方程组求解![]() ,推出
,推出![]() ,即可得到椭圆的方程.
,即可得到椭圆的方程.
(2)存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() .设点
.设点![]() ,
,![]() ,
,![]() ,
,![]() ,将直线
,将直线![]() 的方程
的方程![]() 代入
代入![]() ,化简,利用韦达定理,结合向量的数量积为0,转化为:
,化简,利用韦达定理,结合向量的数量积为0,转化为:![]() .求解即可.
.求解即可.
解:(1)设椭圆的焦半距为c,则由题设,得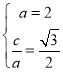 ,解得
,解得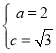 ,
,
所以![]() ,故所求椭圆C的方程为
,故所求椭圆C的方程为![]()
(2)存在实数k使得以线段![]() 为直径的圆恰好经过坐标原点O.理由如下:
为直径的圆恰好经过坐标原点O.理由如下:
设点![]() ,
,![]() ,将直线
,将直线![]() 的方程
的方程![]() 代入
代入![]() ,
,
并整理,得![]() .(*)
.(*)
则![]() ,
,![]()
因为以线段![]() 为直径的圆恰好经过坐标原点O,所以
为直径的圆恰好经过坐标原点O,所以![]() ,即
,即![]() .
.
又![]() ,于是
,于是![]() ,
,
解得![]() ,
,
经检验知:此时(*)式的![]() ,符合题意.
,符合题意.
所以当![]() 时,以线段
时,以线段![]() 为直径的圆恰好经过坐标原点O
为直径的圆恰好经过坐标原点O

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
【题目】某小学六年级学生的进行一分钟跳绳检测,现一班二班各有50人,根据检测结果绘出了一班的频数分布表和二班的频率分布直方图.
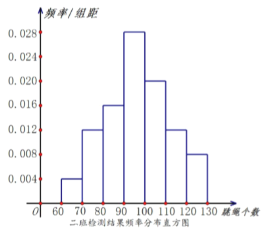
一班检测结果频数分布表:
跳绳个数区间 |
|
|
|
|
|
频数 | 7 | 13 | 20 | 8 | 2 |
(1)根据给出的图表估计一班和二班检测结果的中位数(结果保留两位小数);
(2)跳绳个数不小于100个为优秀,填写下面2×2列联表,并根据列联表判断是否有95%的把握认为检测结果是否优秀与班级有关.
一班 | 二班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式及数据: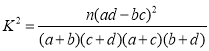 ,
,
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |