题目内容
【题目】已知动圆M与直线
相切，且与圆N：
外切
（1）求动圆圆心M的轨迹C的方程；
（2）点O为坐标原点，过曲线C外且不在y轴上的点P作曲线C的两条切线，切点分别记为A，B，当直线
与
的斜率之积为
时，求证：直线过定点.
【答案】（1）
；（2）见解析
【解析】
（1）直接利用直线与圆的位置关系式，圆和圆的位置关系式的应用求出结果．
（2）利用直线与曲线的相切和一元二次方程根和系数关系式的应用求出结果．
（1）设动圆圆心M（x，y），
由于圆M与直线y=-1相切，且与圆N：
外切．
利用圆心到直线的距离和圆的半径和圆心距之间的关系式，
可知C的轨迹方程为：
（2）设直线
：
，
，
，
因为，
，所以两条切线的斜率分别为
，
，
则直线
的方程是
，
直线
的方程是
.
两个方程联立得P点坐标为
，
，
，由
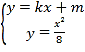联立得：
，
故直线过定点
.
【题目】某小学六年级学生的进行一分钟跳绳检测，现一班二班各有50人，根据检测结果绘出了一班的频数分布表和二班的频率分布直方图.
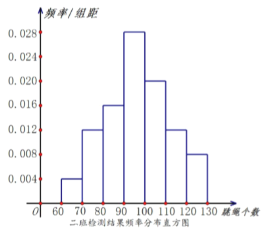
一班检测结果频数分布表：
跳绳个数区间 |
|
|
|
|
|
频数 | 7 | 13 | 20 | 8 | 2 |
（1）根据给出的图表估计一班和二班检测结果的中位数（结果保留两位小数）；
（2）跳绳个数不小于100个为优秀，填写下面2×2列联表，并根据列联表判断是否有95%的把握认为检测结果是否优秀与班级有关.
一班 | 二班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式及数据：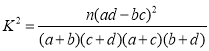
，
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
【题目】为了保障全国第四次经济普查顺利进行，国家统计局从东部选择江苏，从中部选择河北、湖北，从西部选择宁夏，从直辖市中选择重庆作为国家综合试点地区，然后再逐级确定普查区域，直到基层的普查小区，在普查过程中首先要进行宣传培训，然后确定对象，最后入户登记，由于种种情况可能会导致入户登记不够顺利，这为正式普查提供了宝贵的试点经验，在某普查小区，共有50家企事业单位，150家个体经营户，普查情况如下表所示：
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 100 | 50 | 150 |
合计 | 140 | 60 | 200 |
（1）写出选择5个国家综合试点地区采用的抽样方法；
（2）根据列联表判断是否有
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”；
（3）以该小区的个体经营户为样本，频率作为概率，从全国个体经营户中随机选择3家作为普查对象，入户登记顺利的对象数记为
，写出的分布列，并求的期望值．
附：
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
【题目】为方便市民出行，倡导低碳出行.某市公交公司推出利用支付宝和微信扫码支付乘车活动，活动设置了一段时间的推广期，在推广期内采用随机优惠鼓励市民扫码支付乘车.该公司某线路公交车队统计了活动推广期第一周内使用扫码支付的情况，其中
（单位：天）表示活动推出的天次，
（单位：十人次）表示当天使用扫码支付的人次，整理后得到如图所示的统计表1和散点图.
表1：
x | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 |
y | 7 | 12 | 20 | 33 | 54 | 90 | 148 |
（1）由散点图分析后，可用
作为该线路公交车在活动推广期使用扫码支付的人次关于活动推出天次的回归方程，根据表2的数据，求此回归方程，并预报第8天使用扫码支付的人次（精确到整数）.
表2：
|
|
| img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/08/08/88254471/SYS201908080801220877999013_ST/SYS201908080801220877999013_ST.008.png" width="67" height="40" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> |
|
|
4 | 52 | 3.5 | 140 | 2069 | 112 |
表中
，
.
（2）推广期结束后，该车队对此期间乘客的支付情况进行统计，结果如表3.
表3：
支付方式 | 现金 | 乘车卡 | 扫码 |
频率 | 10% | 60% | 30% |
优惠方式 | 无优惠 | 按7折支付 | 随机优惠(见下面统计结果) |
统计结果显示，扫码支付中享受5折支付的频率为
，享受7折支付的频率为
，享受9折支付的频率为
.已知该线路公交车票价为1元，将上述频率作为相应事件发生的概率，记随机变量
为在活动期间该线路公交车搭载乘客一次的收入（单位：元），求的分布列和期望.
参考公式：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
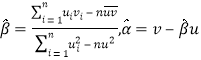参考数据：
，
，
.
