题目内容
(本小题满分14分)
已知函数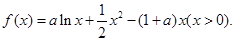
(1)求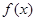 的单调区间;
的单调区间;
(2)若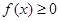 在
在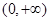 内恒成立,求实数a的取值范围;
内恒成立,求实数a的取值范围;
(3)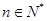 ,求证:
,求证: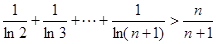
已知函数
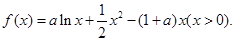
(1)求
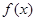 的单调区间;
的单调区间;(2)若
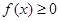 在
在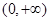 内恒成立,求实数a的取值范围;
内恒成立,求实数a的取值范围;(3)
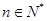 ,求证:
,求证: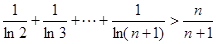
(1) 当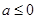 时,
时,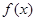 在
在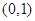 递减,在
递减,在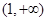 递增;
递增;
当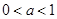 时,
时,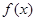 在
在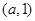 递减,在
递减,在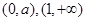 递增;
递增;
当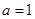 时,
时,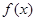 在
在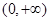 递增;
递增;
当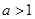 时,
时,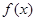 在
在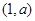 递减,在
递减,在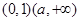 递增。
递增。
(2)构造函数,结合导数的符号判定函数单调性,然后分析得到不等式的证明。
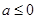 时,
时,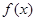 在
在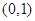 递减,在
递减,在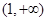 递增;
递增;当
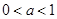 时,
时,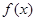 在
在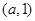 递减,在
递减,在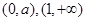 递增;
递增;当
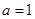 时,
时,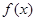 在
在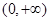 递增;
递增;当
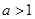 时,
时,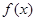 在
在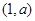 递减,在
递减,在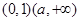 递增。
递增。(2)构造函数,结合导数的符号判定函数单调性,然后分析得到不等式的证明。
试题分析:解:
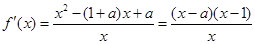
(1)当
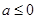 时,
时,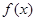 在
在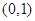 递减,在
递减,在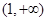 递增;
递增;当
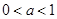 时,
时,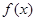 在
在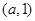 递减,在
递减,在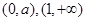 递增;
递增;当
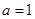 时,
时,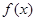 在
在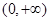 递增;
递增;当
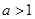 时,
时,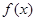 在
在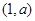 递减,在
递减,在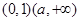 递增。
递增。(2)
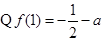 当
当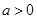 时,
时, ,此时
,此时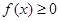 不成立。
不成立。当
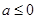 时,由(1)
时,由(1)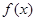 在
在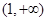 上的最小值为
上的最小值为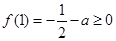
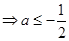
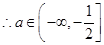 。
。(3)由(2)知
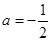 时,
时,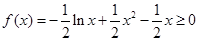
即
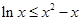 (
(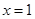 取等)
取等) 当
当 时,
时,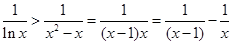
令
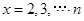 则有
则有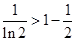 ;
; …
…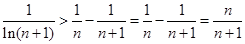
点评:解决的关键是对于导数符号与函数单调性的关系的运用,求解单调区间,同时利用不等式恒成立求解函数的 最值的转化思想,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
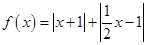 .
.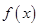 的图象,写出函数
的图象,写出函数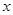 的不等式
的不等式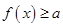
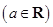 .
.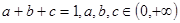 ,求证:
,求证: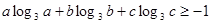 ;
;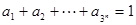 ,
,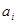 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: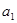
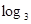
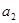
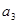
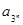
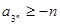
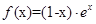 的单调递减区间 .
的单调递减区间 . 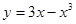 的单调递增区间是
的单调递增区间是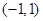
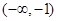
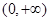
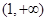
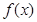
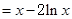 单调递减区间是 。
单调递减区间是 。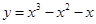 的单调递增区间为______________ 递减区间为____________
的单调递增区间为______________ 递减区间为____________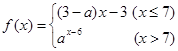 ,若数列
,若数列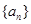 满足
满足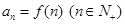 ,且对任意正整数
,且对任意正整数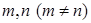 都有
都有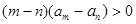 成立,则实数
成立,则实数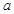 的取值范围是( )
的取值范围是( )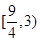
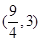
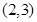
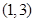
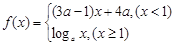 是(-
是(-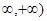 上的减函数,那么
上的减函数,那么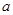 的取值范围是________
的取值范围是________