题目内容
已知函数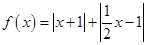 .
.
(1)画出函数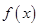 的图象,写出函数
的图象,写出函数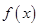 的单调区间;
的单调区间;
(2)解关于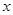 的不等式
的不等式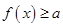
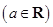 .
.
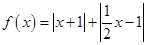 .
.(1)画出函数
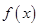 的图象,写出函数
的图象,写出函数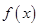 的单调区间;
的单调区间;(2)解关于
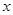 的不等式
的不等式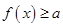
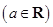 .
.(1) 单调递减区间是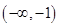 ,单调递增区间是
,单调递增区间是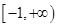 .
.
(2) 当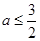 时,
时,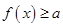 恒成立,即不等式的解为
恒成立,即不等式的解为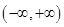 ;
;
当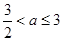 时,不等式的解为
时,不等式的解为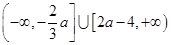 ;
;
当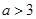 时,不等式的解为
时,不等式的解为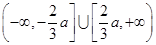 .
.
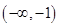 ,单调递增区间是
,单调递增区间是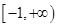 .
.(2) 当
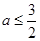 时,
时,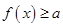 恒成立,即不等式的解为
恒成立,即不等式的解为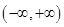 ;
; 当
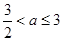 时,不等式的解为
时,不等式的解为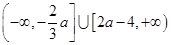 ;
; 当
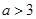 时,不等式的解为
时,不等式的解为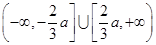 .
.试题分析:解析:
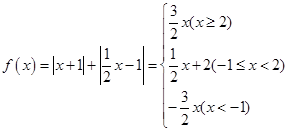 .
. 画出函数
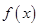 的图象如图中的折线,其单调递减区间是
的图象如图中的折线,其单调递减区间是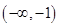 ,单调递增区间是
,单调递增区间是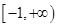 .
.(2)结合图象可知:
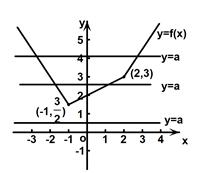
当
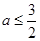 时,
时,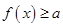 恒成立,即不等式的解为
恒成立,即不等式的解为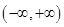 ;
; 当
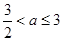 时,不等式的解为
时,不等式的解为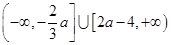 ;
; 当
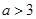 时,不等式的解为
时,不等式的解为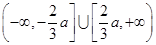 .
. 点评:利用去掉绝对值符号来得到函数解析式,结合函数性质来得到不等式的解集,属于基础题。

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
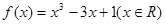 。
。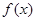 在点
在点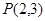 处的切线方程;
处的切线方程;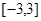 的最大值与最小值。
的最大值与最小值。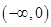 上单调递增的函数是 .
上单调递增的函数是 .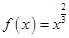 ②
②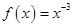 ③
③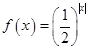 ④
④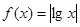
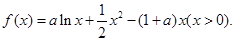
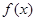 的单调区间;
的单调区间;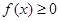 在
在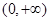 内恒成立,求实数a的取值范围;
内恒成立,求实数a的取值范围;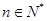 ,求证:
,求证: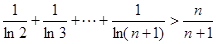
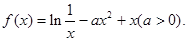
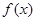 是定义域上的单调函数,求
是定义域上的单调函数,求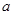 的取值范围;
的取值范围;
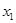 、
、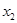 ,证明:
,证明: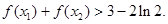
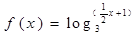 的单调递增区间为_______________.
的单调递增区间为_______________.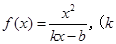 ,
,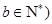 ,满足
,满足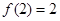 ,
,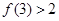 .
.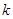 ,
,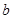 的值;
的值;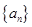 的前
的前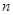 项和为
项和为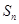 ,且有
,且有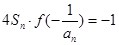 ,设
,设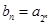 ,求数列
,求数列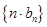 的前
的前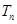 ;
;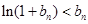 .
.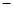
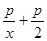 在[1,+∞)上是增函数,则实数p的取值范围是( )
在[1,+∞)上是增函数,则实数p的取值范围是( )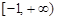
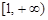
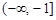
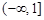
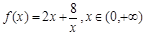 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下: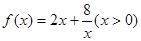 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数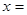 时,
时,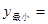 .
.