题目内容
(本小题满分13分)椭圆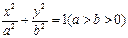 的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.(Ⅰ)如果点A在圆
的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.(Ⅰ)如果点A在圆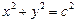 (c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;(Ⅱ)若函数
(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;(Ⅱ)若函数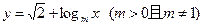 的图象,无论m为何值时恒过定点(b,a),求
的图象,无论m为何值时恒过定点(b,a),求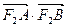 的取值范围.
的取值范围.
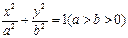 的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.(Ⅰ)如果点A在圆
的左、右焦点分别为F1、F2,过F1的直线l与椭圆交于A、B两点.(Ⅰ)如果点A在圆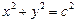 (c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;(Ⅱ)若函数
(c为椭圆的半焦距)上,且|F1A|=c,求椭圆的离心率;(Ⅱ)若函数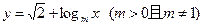 的图象,无论m为何值时恒过定点(b,a),求
的图象,无论m为何值时恒过定点(b,a),求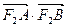 的取值范围.
的取值范围.(Ⅰ) (Ⅱ) 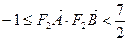
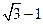
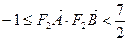
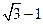
:(1)∵点A在圆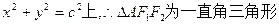 ,
,
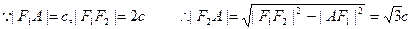
由椭圆的定义知:|AF1|+|AF2|=2a,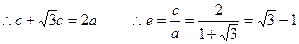
(2)∵函数
∴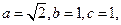 点F1(-1,0),F2(1,0),
点F1(-1,0),F2(1,0),
①若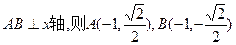 ,
,
∴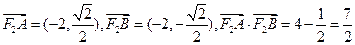
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由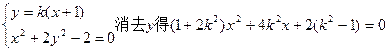 …………(*)
…………(*)
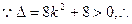 方程(*)有两个不同的实根.
方程(*)有两个不同的实根.
设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根

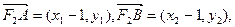
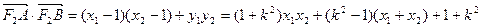
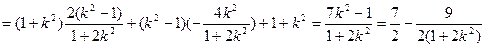
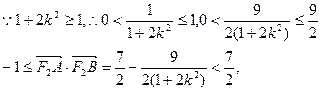
由①②知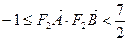
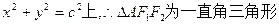 ,
,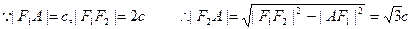
由椭圆的定义知:|AF1|+|AF2|=2a,
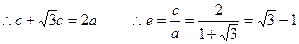
(2)∵函数

∴
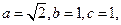 点F1(-1,0),F2(1,0),
点F1(-1,0),F2(1,0), ①若
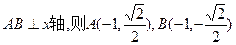 ,
,∴
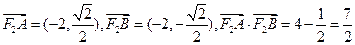
②若AB与x轴不垂直,设直线AB的斜率为k,则AB的方程为y=k(x+1)
由
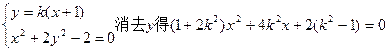 …………(*)
…………(*)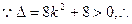 方程(*)有两个不同的实根.
方程(*)有两个不同的实根.设点A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根

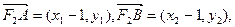
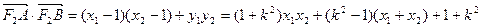
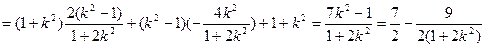
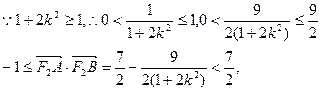
由①②知
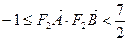

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
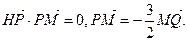
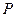 是曲线
是曲线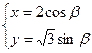 上一点,
上一点,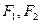 是该曲线的两个焦点,若
是该曲线的两个焦点,若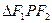 内角平分线的交点到三边上的距离为1,,则
内角平分线的交点到三边上的距离为1,,则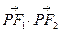 的值为
的值为 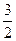
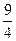
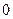
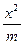 +
+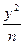 =1与双曲线
=1与双曲线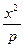 -
-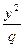 =1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= .
=1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= .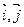 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量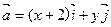 ,
,
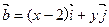 ,且
,且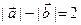 .(1)求满足上述条件的点
.(1)求满足上述条件的点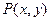 的轨迹方程;(2)设
的轨迹方程;(2)设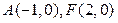 ,问是否存在常数
,问是否存在常数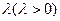 ,使得
,使得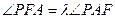 恒成立?证明你的结论.
恒成立?证明你的结论.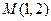 ,它们在
,它们在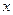 轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .
轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .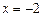 ,且直线l与x轴交于点M,圆
,且直线l与x轴交于点M,圆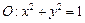 与x轴交于
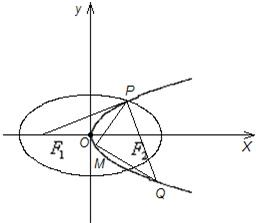
与x轴交于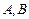 两点(如图).
两点(如图).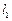 交圆于
交圆于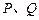 两点,且圆孤
两点,且圆孤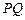 恰为圆周的
恰为圆周的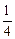 ,求直线
,求直线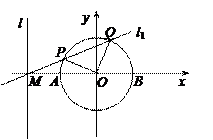
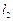 交(II)中的一个椭圆于
交(II)中的一个椭圆于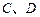 两点,其中
两点,其中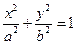 (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B,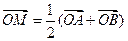 ,且
,且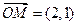 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,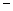 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率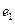 ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为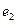 ,记
,记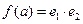 ,求
,求 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.