题目内容
设向量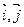
为直角坐标平面内x轴，y轴正方向上的单位向量．若向量
，
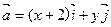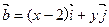，且
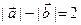．（1）求满足上述条件的点
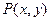的轨迹方程；（2）设
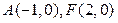，问是否存在常数
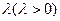，使得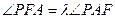
恒成立？证明你的结论．
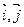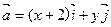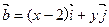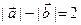为直角坐标平面内x轴，y轴正方向上的单位向量．若向量，，且．（1）求满足上述条件的点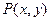的轨迹方程；（2）设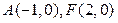，问是否存在常数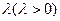，使得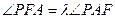恒成立？证明你的结论．（1）
（2）略
（2）略（1）由条件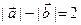可知：
.
由双曲线定义，得点P的轨迹方程：.…………………4分
（2）在第一象限内作
，此时
．………………………………….……6分
以下证明当PF与x轴不垂直且P在第一象限时，
恒成立．
由
，得
.
代入上式并化简得
……10分
由对称性知，当P在第四象限时，同样成立．
故存在常数，使得恒成立．………………….………12分
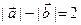可知：.由双曲线定义，得点P的轨迹方程：
.…………………4分（2）在第一象限内作
，此时 ．………………………………….……6分以下证明当PF与x轴不垂直且P在第一象限时，
恒成立．由
，得.代入上式并化简得
……10分由对称性知，当P在第四象限时，同样成立．
故存在常数
，使得恒成立．………………….………12分
练习册系列答案
相关题目
所表示的曲线是 （ ）
：
，直线
交
两点，
是线段
的中点，过
轴的垂线交
．（1）证明：抛物线
使NA
NB，若存在，求
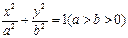的左、右焦点分别为F1、F2，过F1的直线l与椭圆交于A、B两点.（Ⅰ）如果点A在圆
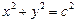（c为椭圆的半焦距）上，且|F1A|=c，求椭圆的离心率；（Ⅱ）若函数
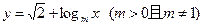的图象，无论m为何值时恒过定点（b，a），求
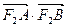的取值范围.
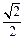的椭圆，点F为其右焦点．
. 若直线l与曲线S同时满足下列两个条件：①直线l与曲线S相切且至少有两个切点；②对任意x∈R都有
. 则称直线l为曲线S的“上夹线”．（Ⅰ）已知函数
．求证：
为曲线
的“上夹线”．
的“上夹线”的方程，并给出证明．
，
且有
，则
点的轨迹是（ ）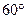
的直线被圆学
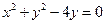所截得的弦长为科网
