题目内容
【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下,请根据此解答如下问题: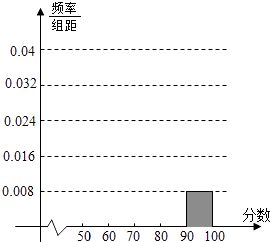
(1)求班级的总人数;
(2)将频率分布表及频率分布直方图的空余位置补充完整;
(3)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100)之间的概率.
分组 | 频数 | 频率 |
[50,60) | 0.08 | |
[60,70) | 7 | |
[70,80) | 10 | |
[80,90) | ||
[90,100) | 2 |
【答案】
(1)解:分数在[90,100)的频率为0.008×10=0.08,频数为2,
∴全班人数为 ![]() =25
=25
(2)解:[50,60)频数为2;[60,70)频率为 ![]() =0.28;[70,80)频率为
=0.28;[70,80)频率为 ![]() =0.4;[80,90)频数为4,频率为0.16,频率分布表
=0.4;[80,90)频数为4,频率为0.16,频率分布表
分组 | 频数 | 频率 |
[50,60) | 2 | 0.08 |
[60,70) | 7 | 0.28 |
[70,80) | 10 | 0.40 |
[80,90) | 4 | 0.16 |
[90,100) | 2 | 0.08 |
频率分布直方图
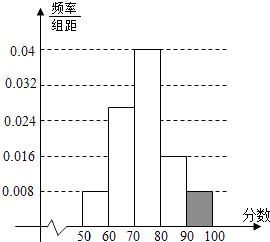 ;
;
(3)解:将[80,90)之间的频数为4,[90,100)之间的频数为2,
在[80,100)之间的试卷中任取两份的基本事件为 ![]() =15个,
=15个,
其中,至少有一个在[90,100)之间的基本事件有9个,
故至少有一份分数在[90,100)之间的概率是0.6.
【解析】(1)分数在[90,100)的频率为0.008×10=0.08,频数为2,即可求得本次考试的总人数;(2)[50,60)频数为2;[60,70)频率为 ![]() =0.28;[70,80)频率为
=0.28;[70,80)频率为 ![]() =0.4;[80,90)频数为4,频率为0.16,可得频率分布表及频率分布直方图的空余位置;(3)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
=0.4;[80,90)频数为4,频率为0.16,可得频率分布表及频率分布直方图的空余位置;(3)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
【考点精析】根据题目的已知条件,利用频率分布表和频率分布直方图的相关知识可以得到问题的答案,需要掌握第一步,求极差;第二步,决定组距与组数;第三步,确定分点,将数据分组;第四步,列频率分布表;频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.