��Ŀ����
����Ŀ��ij����100���������ƽ���õ�������λ���ȣ�����[160��180����[180��200����[200.220����[220��240����[240��260����[260��280����[280��300]�����Ƶ�ʷֲ�ֱ��ͼ��ͼʾ�� ������ֱ��ͼ��x��ֵ��
��������ƽ���õ�������������λ����
��������ƽ���õ���Ϊ[220��240����[240��260����[260��280���������û��У��÷ֲ�����ķ�����ȡ10����������ƽ���õ�����[220��240�����û���Ӧ��ȡ���ٻ���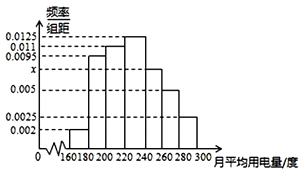
���𰸡��⣺������ֱ��ͼ�����ʣ��ɵ� ��0.002+0.0095+0.011+0.0125+x+0.005+0.0025����20=1
�ã�x=0.0075������ֱ��ͼ��x��ֵ��0.0075��
������ƽ���õ����������� ![]() =230��
=230��
��Ϊ��0.002+0.0095+0.011����20=0.45��0.5��������ƽ���õ�������λ����[220��240���ڣ�
����λ��Ϊa���ɣ�0.002+0.0095+0.011����20+0.0125����a��220��=0.5
�ã�a=224��������ƽ���õ�������λ����224
������ƽ���õ���Ϊ[220��240]���û���0.0125��20��100=25����
��ƽ���õ���Ϊ[240��260�����û���0.0075��20��100=15����
��ƽ���õ���Ϊ[260��280�����û���0.005��20��100=10����
��ȡ����= ![]() =
= ![]() ��
��
������ƽ���õ�����[220��240�����û���Ӧ��ȡ25�� ![]() =5��
=5��
��������������ֱ��ͼ�����������ֱ��ͼ��x��ֵ��������Ƶ�ʷֲ�ֱ��ͼ�������ƽ���õ�������������λ����������ƽ���õ���Ϊ[220��240]���û���25������ƽ���õ���Ϊ[240��260�����û���15������ƽ���õ���Ϊ[260��280�����û���10�����ɴ��������ƽ���õ�����[220��240�����û���Ӧ��ȡ�Ļ�����
�����㾫����ͨ���������Ƶ�ʷֲ�ֱ��ͼ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ�����Խ����⣮

����Ŀ��ijУ����ij���һ�β��Գɼ���Ƶ�ʷֲ����Լ�Ƶ�ʷֲ�ֱ��ͼ�еIJ����������£�����ݴ˽���������⣺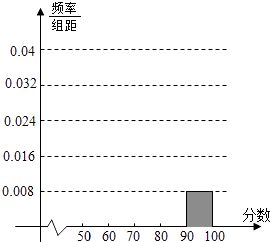
��1����༶����������
��2����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ�Ŀ���λ�ò���������
��3����Ҫ�ӷ�����[80��100��֮����Ծ�����ȡ���ݷ���ѧ��ʧ��������ڳ�ȡ���Ծ��У���������һ�ݷ�����[90��100��֮��ĸ��ʣ�
���� | Ƶ�� | Ƶ�� |
[50��60�� | 0.08 | |
[60��70�� | 7 | |
[70��80�� | 10 | |
[80��90�� | ||
[90��100�� | 2 |