题目内容
【题目】已知圆C的圆心在直线3x+y﹣1=0上，且x轴，y轴被圆C截得的弦长分别为2 
，4 
，若圆心C位于第四象限
（1）求圆C的方程；
（2）设x轴被圆C截得的弦AB的中心为N，动点P在圆C内且P的坐标满足关系式（x﹣1）2﹣y2= 
，求 
的取值范围．
【答案】
（1）解：设圆C的方程为：（x﹣a）2+（y﹣b）2=r2，
根据题意，有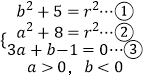 
①﹣②得b2=a2+3，…④
由③④得4a2﹣3a﹣1=0，∵a＞0，解得a=1，b=1﹣3a=﹣2，r2=9，
∴圆C的方程为：（x﹣1）2+（y+2）2=9，
（2）解：在圆C的方程：（x﹣1）2+（y+2）2=9中令y=0，
得A（1﹣ 
，0），B（1+ 
），∴N（1，0）．
∵动点P（x，y）在圆C内，∴（x﹣1）2+（y+2）2＜9…①
将①代入（x﹣1）2﹣y2= 
得﹣ 
，0 
=（1﹣ ﹣x，﹣y）（1+ ﹣x，﹣y）=（x﹣1）2+y2﹣5…②
将（x﹣1）2﹣y2= 代入②得 =2y2﹣ 
．
【解析】（1）设圆C的方程为：（x﹣a）2+（y﹣b）2=r2 ， 根据题意，有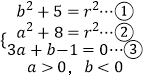
由①②③得a=1，b=1﹣3a=﹣2，r2=9，即可得圆的方程；（2）在圆C的方程：（x﹣1）2+（y+2）2=9中令y=0，得A（1﹣ ，0），B（1+ ），N（1，0）．
将x﹣1）2+（y+2）2＜9．（x﹣1）2﹣y2= 代入 =（1﹣ ﹣x，﹣y）（1+ ﹣x，﹣y）=（x﹣1）2+y2﹣5即可求解．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某城市随机抽取一年（365天）内100天的空气质量指数API的监测数据，结果统计如表：
API | [0，50] | （50，100] | （100，150] | （150，200] | （200，250] | （250，300] | ＞300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
（1）若某企业每天由空气污染造成的经济损失S（单位：元）与空气质量指数API（记为ω）的关系式为： S=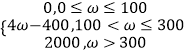 
，试估计在本年内随机抽取一天，该天经济损失S大于200元且不超过600元的概率；
（2）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面2×2列联表，并判断能否有95%的把握认为该市本年空气重度污染与供暖有关？ 附：
P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= 
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
【题目】某校高三某班的一次测试成绩的频率分布表以及频率分布直方图中的部分数据如下，请根据此解答如下问题：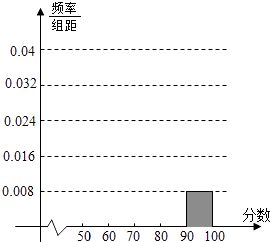
（1）求班级的总人数；
（2）将频率分布表及频率分布直方图的空余位置补充完整；
（3）若要从分数在[80，100）之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在[90，100）之间的概率．
分组 | 频数 | 频率 |
[50，60） | 0.08 | |
[60，70） | 7 | |
[70，80） | 10 | |
[80，90） | ||
[90，100） | 2 |
