题目内容
(本小题满分14分)
已知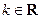 函数
函数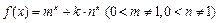 .
.
(I) 若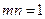 且函数
且函数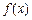 为奇函数,求实数
为奇函数,求实数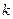 ;
;
(II) 若 试判断函数
试判断函数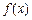 的单调性;
的单调性;
(III) 当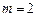 ,
,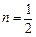 ,
,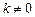 时,求函数
时,求函数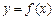 的对称轴或对称中心.
的对称轴或对称中心.
已知
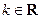 函数
函数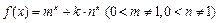 .
.(I) 若
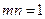 且函数
且函数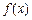 为奇函数,求实数
为奇函数,求实数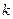 ;
;(II) 若
 试判断函数
试判断函数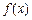 的单调性;
的单调性;(III) 当
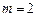 ,
,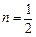 ,
,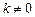 时,求函数
时,求函数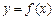 的对称轴或对称中心.
的对称轴或对称中心.解:(1)因为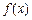 为奇函数,所以
为奇函数,所以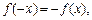
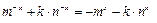 恒成立.
恒成立.
即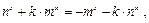
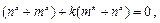
即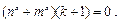 由
由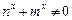 恒成立,得
恒成立,得 …………………………….3分
…………………………….3分
(II)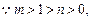
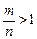 ,
,
∴ 当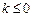 时,显然
时,显然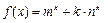 在R上为增函数; ………………………….5分
在R上为增函数; ………………………….5分
当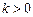 时,
时,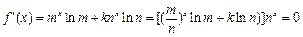 ,
,
由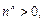 得
得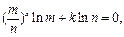 得
得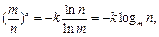 得
得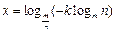 .
.
………………………………………………7分
∴当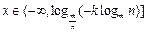 时,
时, 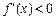 ,
,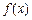 为减函数;
为减函数;
当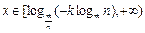 时,
时, 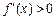 ,
,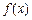 为增函数. ……………………………9分
为增函数. ……………………………9分
(III) 当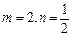 时,
时,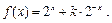
若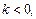
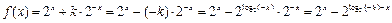 ,
,
则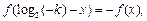
∴函数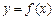 有对称中心
有对称中心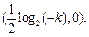 ……………………………………………..12分
……………………………………………..12分
若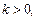
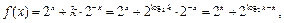
则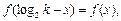
∴函数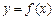 有对称轴
有对称轴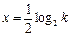 . ……………………………………………..14分
. ……………………………………………..14分
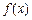 为奇函数,所以
为奇函数,所以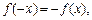
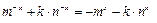 恒成立.
恒成立. 即
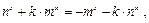
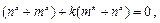
即
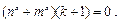 由
由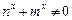 恒成立,得
恒成立,得 …………………………….3分
…………………………….3分(II)
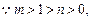
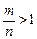 ,
, ∴ 当
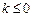 时,显然
时,显然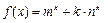 在R上为增函数; ………………………….5分
在R上为增函数; ………………………….5分当
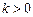 时,
时,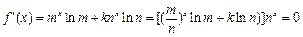 ,
,由
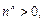 得
得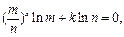 得
得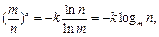 得
得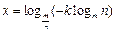 .
.………………………………………………7分
∴当
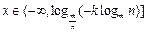 时,
时, 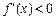 ,
,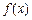 为减函数;
为减函数; 当
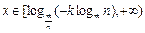 时,
时, 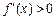 ,
,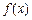 为增函数. ……………………………9分
为增函数. ……………………………9分(III) 当
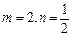 时,
时,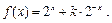
若
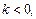
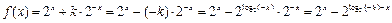 ,
,则
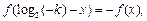
∴函数
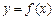 有对称中心
有对称中心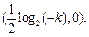 ……………………………………………..12分
……………………………………………..12分若
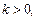
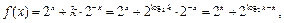
则
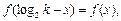
∴函数
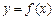 有对称轴
有对称轴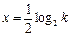 . ……………………………………………..14分
. ……………………………………………..14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
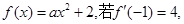 则a等于( )
则a等于( ) ,其中
,其中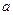 为大于零的常数.
为大于零的常数.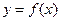 在点(1,
在点(1,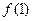 )处的切线与直线
)处的切线与直线 平行,求
平行,求 在区间[1,2]上的最小值.
在区间[1,2]上的最小值. 的图象与x轴的一个交点为A,函数图象在点A处的切线与两条坐标轴围成的面积为 ( )
的图象与x轴的一个交点为A,函数图象在点A处的切线与两条坐标轴围成的面积为 ( ) 在定义域R内可导,若
在定义域R内可导,若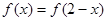 ,且当
,且当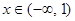 时,
时,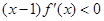 ,设
,设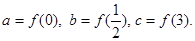 则( )
则( )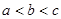
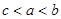
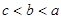

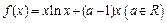 .
.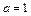 时,求曲线
时,求曲线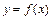 在
在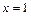 处的切线方程;
处的切线方程;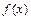 在区间
在区间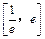 上的最小值;
上的最小值;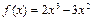 在区间
在区间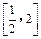 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.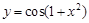 的导数是( )
的导数是( ) B.
B.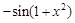 C.
C. D.
D.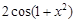
 中任取的一个数,
中任取的一个数,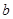 为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线
为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线 交点处的切线相互平行的概率是
交点处的切线相互平行的概率是
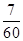
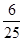
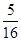
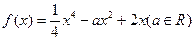 .
.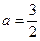 ,求函数
,求函数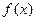 极值;
极值;  ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求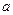 的取值范围.
的取值范围.