题目内容
已知函数 ,其中
,其中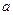 为大于零的常数.
为大于零的常数.
(Ⅰ)若曲线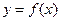 在点(1,
在点(1,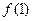 )处的切线与直线
)处的切线与直线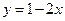 平行,求
平行,求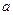 的值;
的值;
(Ⅱ)求函数 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.
 ,其中
,其中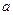 为大于零的常数.
为大于零的常数.(Ⅰ)若曲线
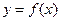 在点(1,
在点(1,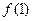 )处的切线与直线
)处的切线与直线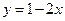 平行,求
平行,求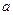 的值;
的值;(Ⅱ)求函数
 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.解: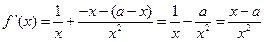 (
( ) ………… 2分
) ………… 2分
(I)因为曲线 在点(1,
在点(1,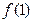 )处的切线与直线
)处的切线与直线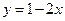 平行,
平行,
所以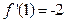 ,即
,即 …………………4分
…………………4分
(II)当 时,
时, 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时 在[1,2]上为增函数
在[1,2]上为增函数
 . ………………………6分
. ………………………6分
当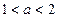 时,由
时,由 得,
得,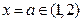
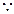 对于
对于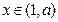 有
有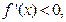
 在[1,a]上为减函数,
在[1,a]上为减函数,
对于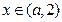 有
有
 在[a,2]上为增函数,
在[a,2]上为增函数,
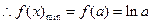 . …………………………………8分
. …………………………………8分
当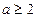 时,
时,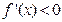 在(1,2)上恒成立, 这时
在(1,2)上恒成立, 这时 在[1,2]上为减函数,
在[1,2]上为减函数,
 .
.
综上, 在[1,2]上的最小值为
在[1,2]上的最小值为
①当 时,
时,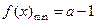 ,
,
②当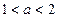 时,
时, ,
,
③当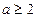 时,
时, . ……………… 12分
. ……………… 12分
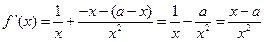 (
( ) ………… 2分
) ………… 2分(I)因为曲线
 在点(1,
在点(1,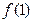 )处的切线与直线
)处的切线与直线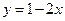 平行,
平行,所以
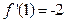 ,即
,即 …………………4分
…………………4分(II)当
 时,
时, 在(1,2)上恒成立,这时
在(1,2)上恒成立,这时 在[1,2]上为增函数
在[1,2]上为增函数 . ………………………6分
. ………………………6分当
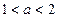 时,由
时,由 得,
得,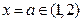
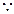 对于
对于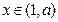 有
有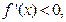
 在[1,a]上为减函数,
在[1,a]上为减函数,对于
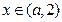 有
有
 在[a,2]上为增函数,
在[a,2]上为增函数,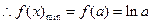 . …………………………………8分
. …………………………………8分当
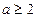 时,
时,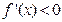 在(1,2)上恒成立, 这时
在(1,2)上恒成立, 这时 在[1,2]上为减函数,
在[1,2]上为减函数, .
.综上,
 在[1,2]上的最小值为
在[1,2]上的最小值为①当
 时,
时,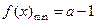 ,
,②当
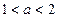 时,
时, ,
,③当
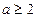 时,
时, . ……………… 12分
. ……………… 12分略

练习册系列答案
相关题目
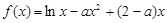 .
.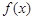 的单调性;
的单调性;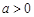 ,证明:当
,证明:当 时,
时,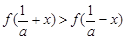 ;
;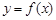 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,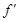 (x0)<0.
(x0)<0.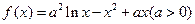 (Ⅰ)求
(Ⅰ)求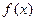 单调区间(Ⅱ)求所有实数
单调区间(Ⅱ)求所有实数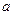 ,使
,使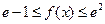 对
对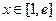 恒成立
恒成立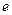 为自然对数的底数
为自然对数的底数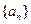 与
与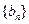 满足:
满足: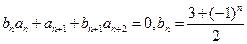 ,
, 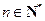 ,且
,且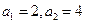 .
.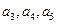 的值;
的值;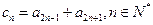
 ,证明:
,证明: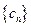 是
是 等比数列;
等比数列; 证明:
证明: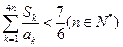 .
.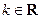 函数
函数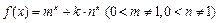 .
.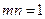 且函数
且函数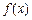 为奇函数,求实数
为奇函数,求实数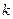 ;
; 试判断函数
试判断函数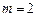 ,
,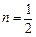 ,
,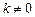 时,求函数
时,求函数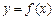 的对称轴或对称中心.
的对称轴或对称中心.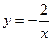 在点
在点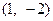 处的切线方程为 .
处的切线方程为 . 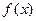 在
在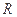 上满足
上满足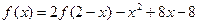 ,则曲线
,则曲线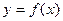 在点
在点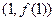 处的切线方程是( )
处的切线方程是( )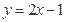
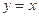
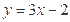
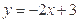
 ,且
,且 ,则
,则 等于
等于


