题目内容
已知函数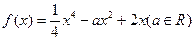 .
.
(I)若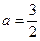 ,求函数
,求函数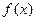 极值;
极值;
(II)设F(x)= ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求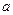 的取值范围.
的取值范围.
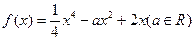 .
.(I)若
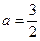 ,求函数
,求函数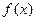 极值;
极值; (II)设F(x)=
 ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求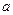 的取值范围.
的取值范围.(Ⅰ)解:当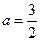 时,
时,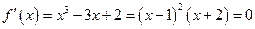
解得: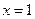 或
或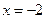 .………………2分
.………………2分
∵当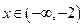 时,
时,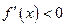 ;
;
当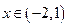 时,
时,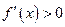 ;
;
当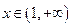 时,
时,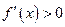 .……………………4分
.……………………4分
∴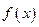 的极小值为
的极小值为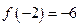 .…………………5分
.…………………5分
(Ⅱ)解法一:
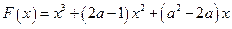 ,
,
即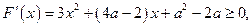 在
在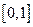 上恒成立,……………7分
上恒成立,……………7分
即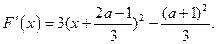
(1)当对称轴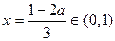 时,
时,
只要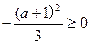 ,即
,即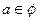 ,…………………9分
,…………………9分
(2)当对称轴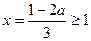 或
或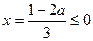 时,
时,
只要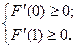
即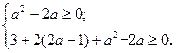 得
得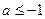 或
或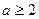 .…………………11分
.…………………11分
综上所述,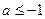 或
或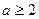 .………………12分
.………………12分
解法二:
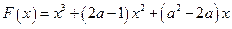 ,
,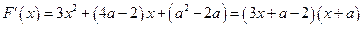 .………………6分
.………………6分
由已知得: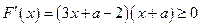 在
在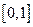 上恒成立,………………8分新课标 第一网
上恒成立,………………8分新课标 第一网
当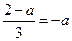 时,即
时,即 时,符合题意;………………9分
时,符合题意;………………9分
当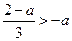 时,即
时,即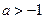 时,只须
时,只须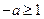 或
或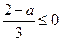 ,
,
∴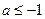 或
或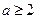 ,∴
,∴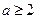 ;……………………10分
;……………………10分
当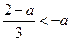 时,即
时,即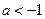 时,只须
时,只须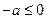 或
或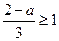 ,
,
∴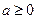 或
或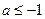 ,∴
,∴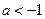 .………………11分
.………………11分
综上所述,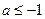 或
或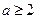 .…………………12分
.…………………12分
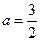 时,
时,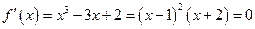
解得:
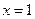 或
或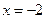 .………………2分
.………………2分∵当
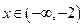 时,
时,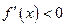 ;
;当
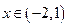 时,
时,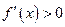 ;
;当
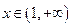 时,
时,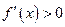 .……………………4分
.……………………4分∴
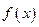 的极小值为
的极小值为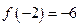 .…………………5分
.…………………5分(Ⅱ)解法一:
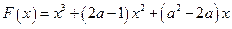 ,
,即
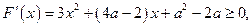 在
在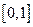 上恒成立,……………7分
上恒成立,……………7分即
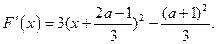
(1)当对称轴
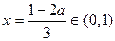 时,
时,只要
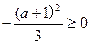 ,即
,即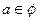 ,…………………9分
,…………………9分(2)当对称轴
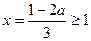 或
或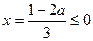 时,
时,只要
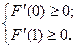
即
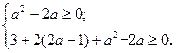 得
得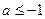 或
或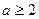 .…………………11分
.…………………11分综上所述,
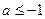 或
或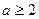 .………………12分
.………………12分解法二:
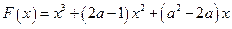 ,
,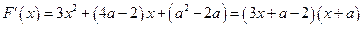 .………………6分
.………………6分 由已知得:
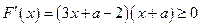 在
在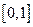 上恒成立,………………8分新课标 第一网
上恒成立,………………8分新课标 第一网当
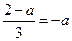 时,即
时,即 时,符合题意;………………9分
时,符合题意;………………9分当
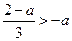 时,即
时,即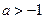 时,只须
时,只须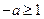 或
或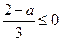 ,
,∴
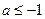 或
或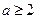 ,∴
,∴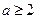 ;……………………10分
;……………………10分当
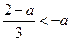 时,即
时,即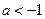 时,只须
时,只须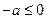 或
或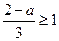 ,
,∴
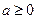 或
或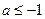 ,∴
,∴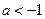 .………………11分
.………………11分综上所述,
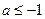 或
或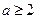 .…………………12分
.…………………12分略

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
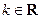 函数
函数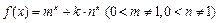 .
.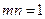 且函数
且函数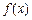 为奇函数,求实数
为奇函数,求实数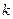 ;
; 试判断函数
试判断函数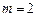 ,
,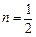 ,
,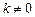 时,求函数
时,求函数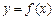 的对称轴或对称中心.
的对称轴或对称中心.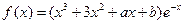 .
.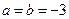 时,求
时,求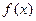 的单调区间;
的单调区间;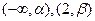 单调增加,在
单调增加,在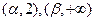 单调减少,证明:
单调减少,证明: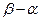 <6.
<6.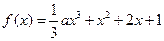 .
.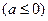
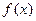 在
在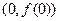 处的切线方程;
处的切线方程;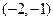 上单调减,且在
上单调减,且在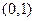 上单调增,求实数
上单调增,求实数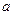 的取值范围;
的取值范围;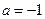 时,若
时,若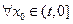 ,函数
,函数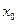 处的切线垂直,求
处的切线垂直,求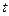 的最小值.
的最小值.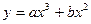 ,当x=
,当x= 1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。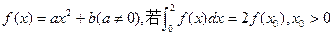 ,则
,则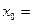 。
。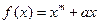 的导函数
的导函数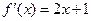 ,则数列
,则数列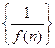 (n∈N*)的前n项和是
(n∈N*)的前n项和是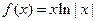 的图像是:( )
的图像是:( )
 B C D
B C D