题目内容
已知一组曲线 中任取的一个数,
中任取的一个数,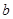 为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线
为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线 交点处的切线相互平行的概率是
交点处的切线相互平行的概率是
 中任取的一个数,
中任取的一个数,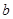 为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线
为1,3,5,7中任取的一个数,从这些曲线中任意抽取两条,它们在与直线 交点处的切线相互平行的概率是
交点处的切线相互平行的概率是A. | B.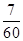 | C.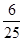 | D.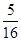 |
A
分析:由题意知,所有抛物线条数是4×4=16条,从16条中任取两条的方法数是C162=120,其中与直线x=1交点处的切线的斜率为k=a+b,由与切线相互平行,可得斜率相等,讨论a+b的取值,从而可求
解:a为2,4,6,8中任取一数,b为1,3,5,7中任取一数的曲线y=
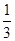 ax3+bx+1,共16条,从这些曲线中任意抽取两条共C162种
ax3+bx+1,共16条,从这些曲线中任意抽取两条共C162种∵y=
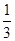 ax3+bx+1,
ax3+bx+1,∴y′=ax2+b,
∴在与直线x=1交点处的切线的斜率为k=a+b因为切线相互平行,所以斜率相等,即a+b相等,
当a+b=5时,共(2,3),(4,1)两组,
当a+b=7时,共(2,5),(4,3),(6,1)三组,
当a+b=9时,共(2,7),(4,5),(6,3),(8,1)四组,
所以切线平行的曲线共C22+C32+C42,所以其概率为
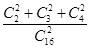 =
=
故选A

练习册系列答案
相关题目
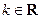 函数
函数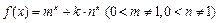 .
.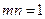 且函数
且函数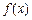 为奇函数,求实数
为奇函数,求实数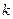 ;
; 试判断函数
试判断函数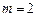 ,
,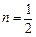 ,
,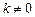 时,求函数
时,求函数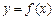 的对称轴或对称中心.
的对称轴或对称中心.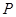 是曲线
是曲线 上的一个动点,则点
上的一个动点,则点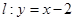 的距离的最小值为( )
的距离的最小值为( )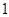
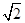
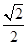
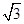
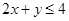 与
与 所确定的平面区域被直线
所确定的平面区域被直线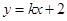 分为面积相等的两部分,则k的值是( )
分为面积相等的两部分,则k的值是( )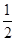
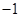
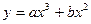 ,当x=
,当x= 1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。 ,且
,且 ,则
,则 等于
等于



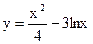 的一条切线的斜率为
的一条切线的斜率为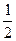 ,则切点的纵坐标为 ▲
,则切点的纵坐标为 ▲ 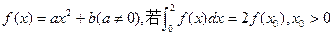 ,则
,则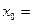 。
。