题目内容
17.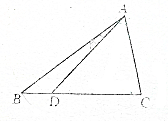 如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.
如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.
分析 由题意可得tanα=$\frac{3BC}{4AC}$,tan(α+β)=$\frac{BC}{AC}$,结合tanα=7tanβ,可得$\frac{\frac{8}{7}tanα}{1-tanα•\frac{1}{7}tanα}$=$\frac{4}{3}$tanα,求得tanα 的值,可得α的值.
解答 解:由题意可得tanα=$\frac{\frac{3}{4}BC}{AC}$=$\frac{3BC}{4AC}$,tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{BC}{AC}$,
又tanα=7tanβ,可得$\frac{\frac{8}{7}tanα}{1-tanα•\frac{1}{7}tanα}$=$\frac{4}{3}$tanα,
∴tanα=1,∴α=$\frac{π}{4}$.
点评 本题主要考查直角三角形中边角关系,两角和差的正切公式,属于基础题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
7.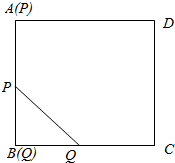 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
6.在平面直角坐标系xOy中,已知抛物线x2=y的焦点为F,点P1(1,1),Qn(n,n2)(n∈N*),连接OP1,作抛物线的切线l1,使之与直线OP1平行,所得切点记为P2(a2,a${\;}_{2}^{2}$)再作抛物线的切线l2,使之与直线OP2平行,所得切点记为P3(a3,a${\;}_{3}^{2}$)…以此类推,得到数列{an},若a1=1,数列{bn}满足|QnF|=nbn+$\frac{1}{4}$,则数列{anbn}的前n项和为( )
| A. | (n-1)•2n+1 | B. | $\frac{n+2}{{2}^{n-1}}$-2 | C. | $\frac{2-n}{{2}^{n-1}}$ | D. | 4-$\frac{n+2}{{2}^{n-1}}$ |
11.复数$\frac{5}{i-2}$的共轭复数是( )
| A. | 2+i | B. | -2-i | C. | -2+i | D. | 2-i |