题目内容
20.已知等差数列{an}的前n项和为Sn,且满足S5=5S2,a2n+1=2an+1(n∈N*),正项等比数列{bn}满足b2=a2,b6=a8,数列{cn}满足cn=$\left\{\begin{array}{l}{{a}_{n},}&{n=2k-1,k∈{N}^{*}}\\{{b}_{n},}&{n=2k.k∈{N}^{*}}\end{array}\right.$.(1)求数列{an},{bn}的通项公式;
(2)求数列{cn}的前n项和为Tn(用n表示);
(3)是否存在正整数m,使得Tm=2cm+2,若存在,求出所有m的值;若不存在,说明理由.
分析 (1)通过S5=5S2得a1=d,通过a2n+1=2an+1得a1-2d+1=0,进而可知an=n.利用q=$\root{4}{\frac{{b}_{8}}{{b}_{2}}}$可知公比,进而可得结论;
(2)通过对n分奇偶数讨论,计算即得结论;
(3)通过对n分奇偶数讨论,计算即得结论.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,
由S5=5S2,得a1=d,
由a2n+1=2an+1得a1-2d+1=0.
∴a1=d=1,an=n.
∴b2=2,b6=8
∵bn>0,
∴公比q=$\root{4}{\frac{{b}_{8}}{{b}_{2}}}$=$\sqrt{2}$,b1=$\sqrt{2}$,
∴bn=$({\sqrt{2})}^{n}$;
(2)∵cn=$\left\{\begin{array}{l}{{a}_{n},}&{n=2k-1,k∈{N}^{*}}\\{{b}_{n},}&{n=2k.k∈{N}^{*}}\end{array}\right.$,
当n为偶数时,Tn=[1+3+5+…+(n-1)]+(2+4+8+…+${2}^{\frac{n}{2}}$)
=$\frac{{n}^{2}}{4}$+$\frac{2-{2}^{\frac{n}{2}+1}}{1-2}$
=$\frac{{n}^{2}}{4}$-2+${2}^{\frac{n}{2}+1}$;
当n为奇数时,Tn=(1+3+5+…+n)+(2+4+8+…+${2}^{\frac{n-1}{2}}$)
=$\frac{(n+1)^{2}}{4}$+$\frac{2-{2}^{\frac{n+1}{2}}}{1-2}$
=$\frac{(n+1)^{2}}{4}$-2+${2}^{\frac{n+1}{2}}$;
∴Tn=$\left\{\begin{array}{l}{\frac{(n+1)^{2}}{4}-2+{2}^{\frac{n+1}{2}},}&{n=2k-1}\\{\frac{{n}^{2}}{4}-2+{2}^{\frac{n}{2}+1},}&{n=2k}\end{array}\right.$;
(3)结论:存在正整数m=4满足题设条件.
理由如下:
当m为偶数时,
$\frac{{m}^{2}}{4}$-2+${2}^{\frac{m}{2}+1}$=2•${2}^{\frac{m}{2}}$+2,即$\frac{{m}^{2}}{4}$=4,
∴m=4;
当m为奇数时,
$\frac{(m+1)^{2}}{4}$-2+${2}^{\frac{m+1}{2}}$=2m+2,
∴4•${2}^{\frac{m+1}{2}}$=24-(m-3)2,
即(m-3)2=24-4•${2}^{\frac{m+1}{2}}$≥0,
∴${2}^{\frac{m+1}{2}}$≤6,∴m=1或3.
∵当m=1时,4≠16,当m=3时,0≠8.
∴当m为奇数时,这样的m不存在.
综上所述:m=4.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案| A. | {1,2} | B. | {1,3} | C. | {2,3} | D. | {2,4} |
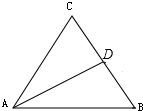 如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )
如图,在△ABC中,D为边BC的中点,则下列结论正确的是( )| A. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{DC}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{DC}$=$\overrightarrow{BC}$ |
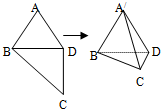 如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).
如图所示,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是(2)(4).