题目内容
5.已知函数f(x)=x(x2-ax+3).(Ⅰ)若x=$\frac{1}{3}$是f(x)的极值点,求f(x)在区间[-1,4]上的最大值与最小值;
(Ⅱ)若f(x)在[1,+∞)上是增函数,求实数a的取值范围.
分析 (Ⅰ)先求出函数f(x)的导数,令f′(x)=0,从而求出函数的单调区间,进而求出函数的最值;
(Ⅱ)问题转化为a≤[$\frac{3}{2}$(x+$\frac{1}{x}$)]最小值即可,设g(x)=x+$\frac{1}{x}$(x≥1),求出函数g(x)的最小值,从而求出a的范围.
解答 解:(Ⅰ)由f(x)=x3-ax2+3x,得:f′(x)=3x2-2ax+3,
由已知得:f′($\frac{1}{3}$)=0,解得:a=5,
∴f(x)=x3-5x2+3x,f′(x)=3x2-10x+3,
由f′(x)=0,解得:x=$\frac{1}{3}$或3,
f(x)与f′(x)在[-1,4]上的变化情况如下:
| x | -1 | (-1,$\frac{1}{3}$) | $\frac{1}{3}$ | ($\frac{1}{3}$,3) | 3 | (3,4) | 4 |
| f′(x) | + | - | + | ||||
| f(x) | -9 | 递增 | $\frac{13}{27}$ | 递减 | -9 | 递增 | -4 |
(Ⅱ)f′(x)=3x2-2ax+3,
由f(x)在[1,+∞)递增,得:
3x2-2ax+3≥0,即;a≤$\frac{3}{2}$(x+$\frac{1}{x}$),
要使上式成立,只要a≤[$\frac{3}{2}$(x+$\frac{1}{x}$)]最小值即可,
设g(x)=x+$\frac{1}{x}$(x≥1),
由于g(x)在[1,+∞)是递增,
∴g(x)最小值=2,
∴a≤3,
即a的取值范围是(-∞,3].
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,是一道中档题.

练习册系列答案
相关题目
16.已知条件p:x>1,q:$\frac{1}{x}$<1,则¬p是¬q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,在某次考试成绩统计中,某老师为了对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行分析,随机挑选了8位同学,得到他们的两科成绩偏差数据如下:
(Ⅰ)若x与y之间具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(Ⅱ)若该次考试该班数学平均分为120分,物理平均分为91.5分,试由(1)的结论预测数学成绩为128分的同学的物理成绩.
参考数据:
$\sum_{i=1}^{8}$xiyi=20×6.5+15×3.5+13×3.5+3×1.5+2×0.5+(-5)×(-0.5)+(-10)×(-2.5)+(-18)×(-3.5)=324
$\sum_{i=1}^{8}$x${\;}_{i}^{2}$=202+152+132+32+22+(-5)2+(-10)2+(-18)2=1256.
14.针对时下的网购热,某单位对“喜欢网购与职工性别是否有关”进行了一次调查,其中男职工有60人,女职工人数是男职工人数的$\frac{1}{2}$,喜欢网购的男职工人数是男职工人数的$\frac{1}{6}$,喜欢网购的女职工人数是女职工人数的$\frac{2}{3}$.
(1)根据以上数据完成下面的2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为喜欢网购与职工性别有关系?
参考数据及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
(1)根据以上数据完成下面的2×2列联表.
| 喜欢网购 | 不喜欢网购 | 总计 | |
| 男职工 | |||
| 女职工 | |||
| 总计 |
参考数据及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
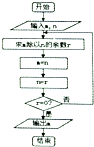 程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.
程序框图如图所示,若输入m,n的值分别为30,18,则程序框图中最后输出的m值等于6.