题目内容
若{an}是等比数列,前n项和Sn=2n-1,则
+
+
+…+
=( )
| a | 21 |
| a | 22 |
| a | 23 |
| a | 2n |
| A.(2n-1)2 | B.
| C.4n-1 | D.
|
当n=1时,a1=S1=2-1=1.
当n≥2时,an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1.
当n=1时也成立.
∴an=2n-1.
∴当n≥2时,
=
=4.
∴数列{
}是等比数列,首项为
=1,公比为4.
∴
+
+
+…+
=
=
(4n-1).
故选:D.
当n≥2时,an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1.
当n=1时也成立.
∴an=2n-1.
∴当n≥2时,
| ||
|
| (2n-1)2 |
| (2n-2)2 |
∴数列{
| a | 2n |
| a | 21 |
∴
| a | 21 |
| a | 22 |
| a | 23 |
| a | 2n |
| 4n-1 |
| 4-1 |
| 1 |
| 3 |
故选:D.

练习册系列答案
相关题目
 的前
的前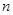 项和为
项和为 ,对任意的正整数
,对任意的正整数 成立,记
成立,记 .(1)(1)求数列
.(1)(1)求数列 的通项公式;
的通项公式; ,是否存在正整数
,是否存在正整数 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ,设数列
,设数列 的前
的前 ,求证:对于
,求证:对于 都有
都有